Evaluate the integral of (x^2 + 4x + 2) / (6x) dx.
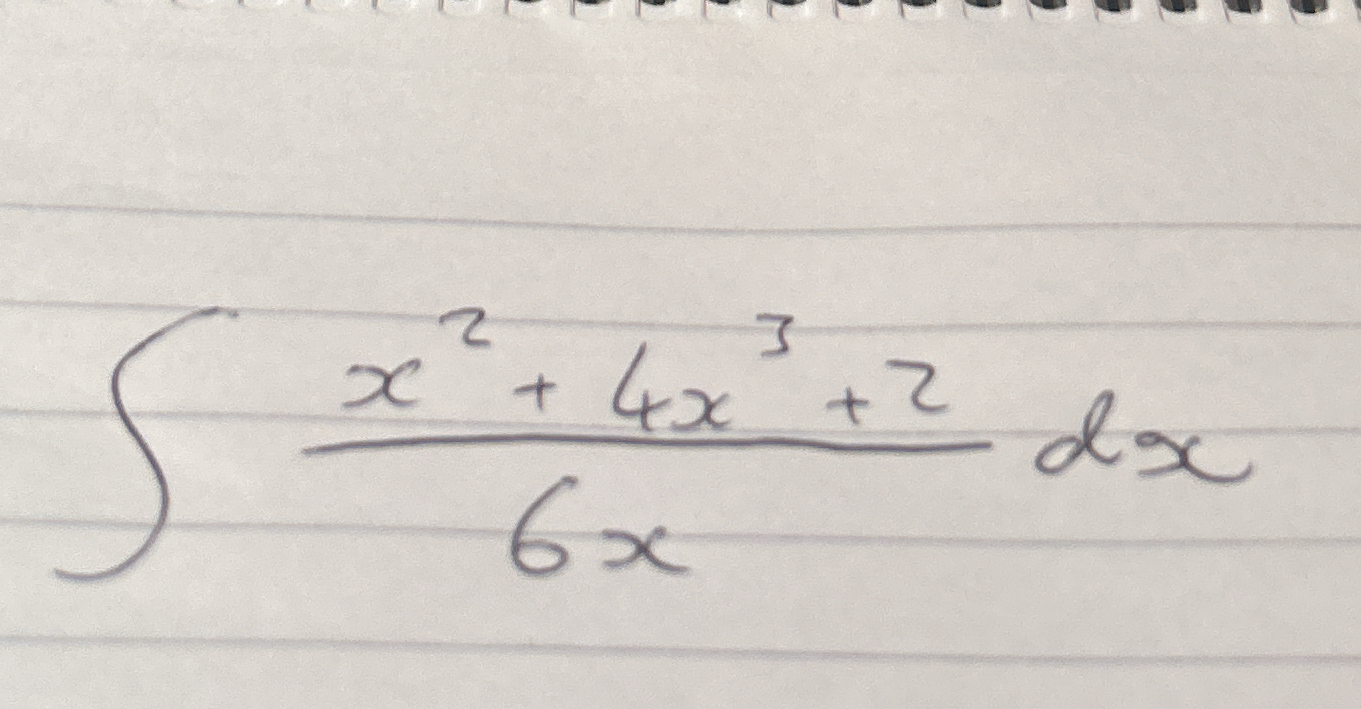
Understand the Problem
The question is asking to evaluate the integral of the expression (x² + 4x + 2) / (6x) with respect to x.
Answer
The result of the integral is $$ \frac{x^2}{12} + \frac{2}{3}x + \frac{1}{3} \ln|x| + C. $$
Answer for screen readers
The integral evaluates to $$ \frac{x^2}{12} + \frac{2}{3}x + \frac{1}{3} \ln|x| + C. $$
Steps to Solve
-
Simplify the integrand Start by separating the terms in the integrand. We can rewrite $$ \frac{x^2 + 4x + 2}{6x} $$ as $$ \frac{x^2}{6x} + \frac{4x}{6x} + \frac{2}{6x}. $$ This simplifies to $$ \frac{x}{6} + \frac{4}{6} + \frac{2}{6x} $$ or $$ \frac{x}{6} + \frac{2}{3} + \frac{1}{3x}. $$
-
Rewrite the integral Now, the integral can be rewritten as: $$ \int \left( \frac{x}{6} + \frac{2}{3} + \frac{1}{3x} \right) dx. $$
-
Integrate each term Integrate each term separately:
- For $\frac{x}{6}$, the integral is $$ \frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12}. $$
- For $\frac{2}{3}$, the integral is $$ \frac{2}{3}x. $$
- For $\frac{1}{3x}$, the integral is $$ \frac{1}{3} \ln|x|. $$
- Combine the results Combining the results of the integrals gives: $$ \int \frac{x^2 + 4x + 2}{6x} , dx = \frac{x^2}{12} + \frac{2}{3} x + \frac{1}{3} \ln|x| + C, $$ where ( C ) is the constant of integration.
The integral evaluates to $$ \frac{x^2}{12} + \frac{2}{3}x + \frac{1}{3} \ln|x| + C. $$
More Information
This integral combines polynomial and logarithmic terms, representing the area under the curve defined by the initial expression. Integrating rational functions is common in calculus and helps in finding areas and determining antiderivatives.
Tips
- Forgetting to add the constant of integration ( C ).
- Misapplying the rules of logarithmic integration, particularly with ( \frac{1}{x} ).
