Evaluate the integral from -1 to 1 of (12x^5 + 12x^2) dx.
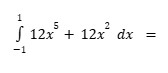
Understand the Problem
The question is asking to evaluate the definite integral of the function 12x^5 + 12x^2 from -1 to 1. This involves finding the antiderivative and then applying the limits of integration.
Answer
$$ 8 $$
Answer for screen readers
The final answer is $$ \int_{-1}^{1} (12x^{5} + 12x^{2}) , dx = 8 $$
Steps to Solve
- Find the Antiderivative To evaluate the definite integral, we first need to find the antiderivative of the function (12x^5 + 12x^2).
The antiderivative is: $$ F(x) = \int (12x^5 + 12x^2) , dx = 12 \cdot \frac{x^6}{6} + 12 \cdot \frac{x^3}{3} = 2x^6 + 4x^3 $$
- Apply the Limits of Integration Next, we will apply the limits of integration from (-1) to (1). This means we need to evaluate (F(1)) and (F(-1)):
-
Calculate (F(1)): $$ F(1) = 2(1)^6 + 4(1)^3 = 2 \cdot 1 + 4 \cdot 1 = 2 + 4 = 6 $$
-
Calculate (F(-1)): $$ F(-1) = 2(-1)^6 + 4(-1)^3 = 2 \cdot 1 + 4 \cdot (-1) = 2 - 4 = -2 $$
- Subtract the Results Now we subtract the two results: $$ \int_{-1}^{1} (12x^{5} + 12x^{2}) , dx = F(1) - F(-1) = 6 - (-2) = 6 + 2 = 8 $$
The final answer is $$ \int_{-1}^{1} (12x^{5} + 12x^{2}) , dx = 8 $$
More Information
The integral represents the area under the curve of the function (12x^5 + 12x^2) from (-1) to (1). Since (12x^5) is an odd function and contributes zero to the integral over symmetric limits while (12x^2) is even, the positive area from the even function is what counts here.
Tips
- Forgetting to correctly apply the limits of integration.
- Confusing the antiderivative with the integrand; ensure to differentiate correctly.
- Miscalculating values for (F(1)) or (F(-1)).
AI-generated content may contain errors. Please verify critical information