Evaluate the integral from 0 to π/2 of sin x / (1 + cos² x) dx.
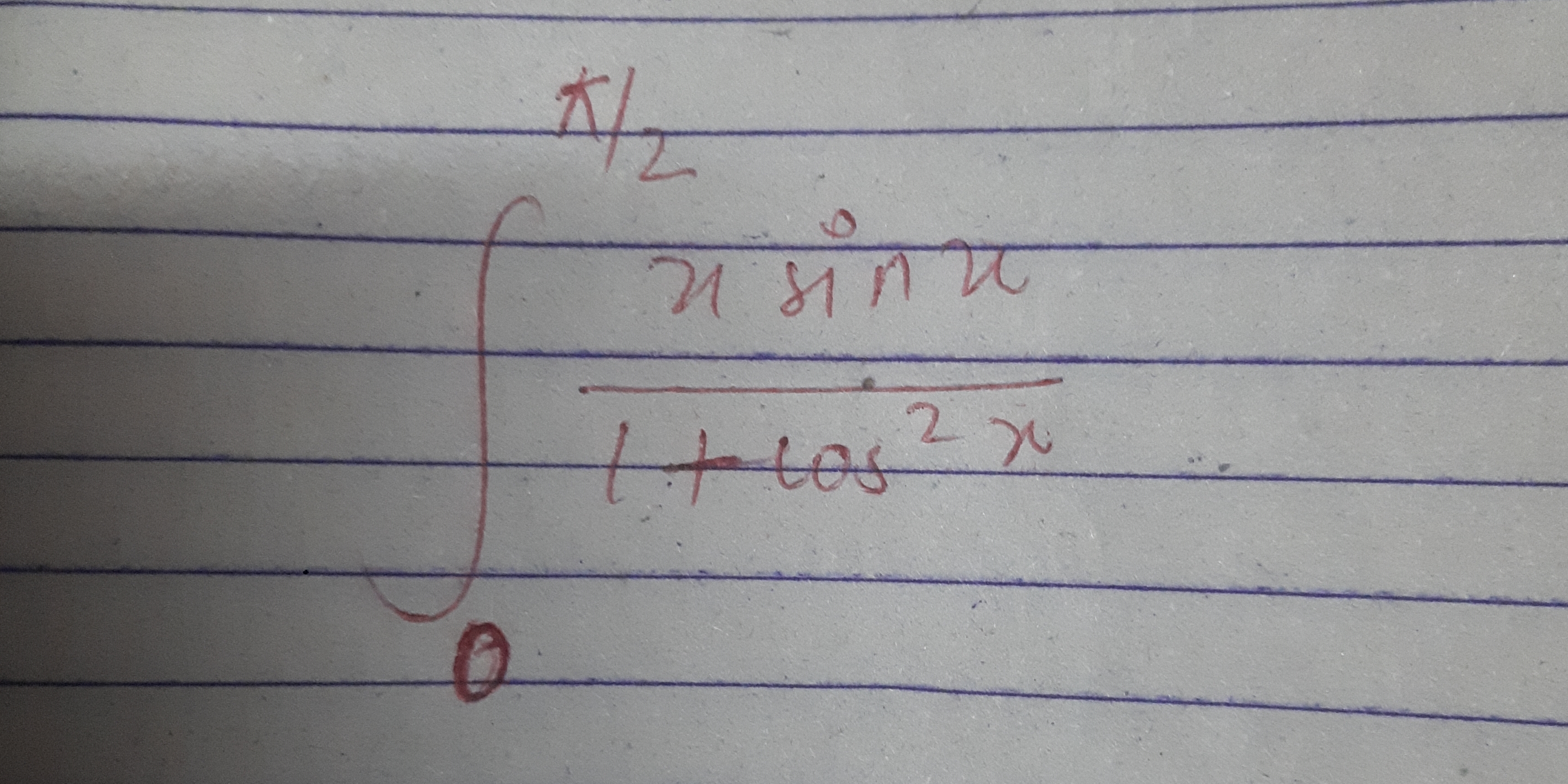
Understand the Problem
The question presents a mathematical integral that needs to be evaluated. The integral is from 0 to π/2 of the function (sin x) / (1 + cos² x) dx. The task requires knowledge of calculus to find its solution.
Answer
$$ I = \frac{\pi}{4} $$
Answer for screen readers
The final answer is: $$ I = \frac{\pi}{4} $$
Steps to Solve
-
Set Up the Integral
We start with the integral we need to evaluate: $$ I = \int_0^{\frac{\pi}{2}} \frac{\sin x}{1 + \cos^2 x} , dx $$ -
Use a Trigonometric Identity
We apply the identity for $\cos^2 x$: $$ \cos^2 x = 1 - \sin^2 x $$
Thus, we can rewrite the integral as: $$ I = \int_0^{\frac{\pi}{2}} \frac{\sin x}{1 + (1 - \sin^2 x)} , dx = \int_0^{\frac{\pi}{2}} \frac{\sin x}{2 - \sin^2 x} , dx $$ -
Substitution Method
Let ( u = \cos x ) then ( du = -\sin x , dx ). The limits change from ( x = 0 ) to ( x = \pi/2 ), thus ( u) goes from ( 1) to ( 0). Therefore: $$ I = \int_1^0 \frac{-1}{2 - (1-u^2)} , du $$
Rearranging gives: $$ I = \int_0^1 \frac{1}{1 + u^2} , du $$ -
Evaluate the Integral
The integral: $$ \int \frac{1}{1 + u^2} , du = \tan^{-1}(u) + C $$
Thus: $$ I = \left[ \tan^{-1}(u) \right]_0^1 = \tan^{-1}(1) - \tan^{-1}(0) $$ -
Calculate the Final Result
We know: $$ \tan^{-1}(1) = \frac{\pi}{4} \quad \text{and} \quad \tan^{-1}(0) = 0 $$ Thus: $$ I = \frac{\pi}{4} - 0 = \frac{\pi}{4} $$
The final answer is: $$ I = \frac{\pi}{4} $$
More Information
The integral $\int \frac{\sin x}{1 + \cos^2 x} , dx$ is a classic problem in calculus, demonstrating the use of substitution and trigonometric identities. The result $\frac{\pi}{4}$ represents a specific area under the curve for the given limits of integration.
Tips
- Forgetting to adjust the limits after substitution.
- Not recognizing the appropriate trigonometric identity to simplify the expression.
- Confusing the integral of $\frac{1}{1 + u^2}$ with other similar integrals.
AI-generated content may contain errors. Please verify critical information