Evaluate the indefinite integral: ∫(x^2 - x + 3 - 1/x) dx
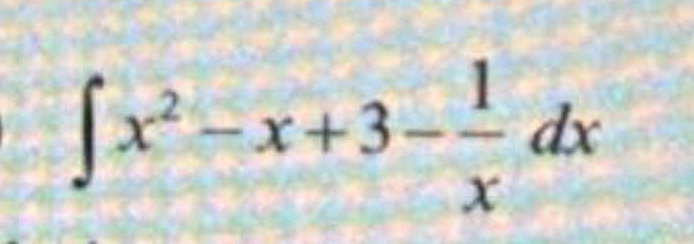
Understand the Problem
The question asks to evaluate the indefinite integral of the function x^2 - x + 3 - 1/x with respect to x. This involves applying basic integration rules to each term of the function.
Answer
$\frac{x^3}{3} - \frac{x^2}{2} + 3x - \ln|x| + C$
Answer for screen readers
$\frac{x^3}{3} - \frac{x^2}{2} + 3x - \ln|x| + C$
Steps to Solve
- Integrate $x^2$
Using the power rule for integration $\int x^n dx = \frac{x^{n+1}}{n+1} + C$, we have:
$\int x^2 dx = \frac{x^{2+1}}{2+1} + C = \frac{x^3}{3} + C$
- Integrate $-x$
Using the power rule again:
$\int -x dx = -\int x^1 dx = -\frac{x^{1+1}}{1+1} + C = -\frac{x^2}{2} + C$
- Integrate $3$
The integral of a constant is the constant times $x$:
$\int 3 dx = 3x + C$
- Integrate $-\frac{1}{x}$
The integral of $\frac{1}{x}$ is $\ln|x|$:
$\int -\frac{1}{x} dx = -\int \frac{1}{x} dx = -\ln|x| + C$
- Combine the results
Adding all the individual integrals together:
$\int (x^2 - x + 3 - \frac{1}{x}) dx = \frac{x^3}{3} - \frac{x^2}{2} + 3x - \ln|x| + C$
$\frac{x^3}{3} - \frac{x^2}{2} + 3x - \ln|x| + C$
More Information
The indefinite integral represents a family of functions that differ by a constant $C$. This constant appears because the derivative of a constant is zero, so when we reverse the process (integration), we need to account for any possible constant term.
Tips
A common mistake is forgetting the constant of integration, $C$. Another common mistake is incorrectly applying the power rule, especially when dealing with terms like $\frac{1}{x}$. Remember that $\int \frac{1}{x} dx = \ln|x| + C$, not $\frac{x^0}{0}$.
AI-generated content may contain errors. Please verify critical information