Evaluate the function f(x, y) = x² + y² over the triangular region with vertices (0, 0), (1, 0), and (0, 1).
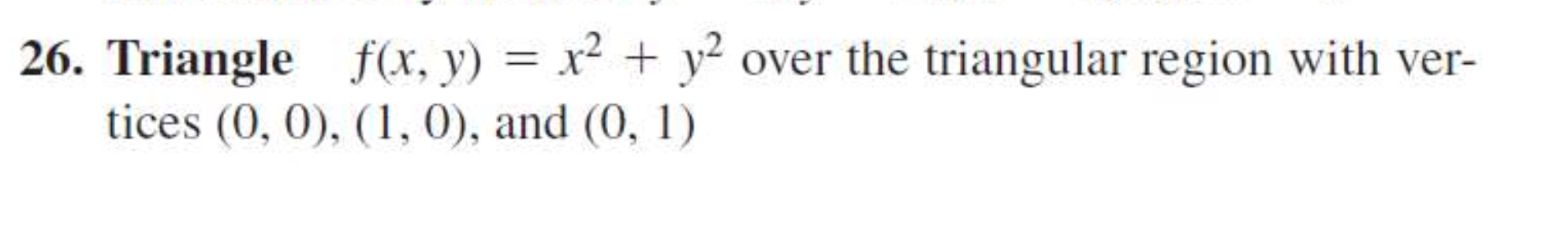
Understand the Problem
The question is asking for the evaluation of the function f(x, y) = x² + y² over a triangular region defined by the vertices (0, 0), (1, 0), and (0, 1). This typically involves double integration over the specified region.
Answer
The result of the double integral over the triangular region is $$ \frac{1}{6} $$.
Answer for screen readers
The final answer is:
$$ \frac{1}{6} $$
Steps to Solve
- Define the Region of Integration
The triangular region is bounded by the vertices (0, 0), (1, 0), and (0, 1). In the Cartesian plane, this creates a right triangle.
- Set Up the Double Integral
The function we want to integrate is $f(x, y) = x^2 + y^2$. The limits for $y$ will be from 0 to $1 - x$ for $x$ ranging from 0 to 1:
$$ \int_{0}^{1} \int_{0}^{1-x} (x^2 + y^2) , dy , dx $$
- Integrate with Respect to $y$ First
Now we compute the inner integral:
$$ \int_{0}^{1-x} (x^2 + y^2) , dy $$
This can be split into two integrals:
$$ \int_{0}^{1-x} x^2 , dy + \int_{0}^{1-x} y^2 , dy $$
The first integral is:
$$ x^2 \cdot y \Big|_{0}^{1-x} = x^2(1-x) $$
The second integral is:
$$ \frac{y^3}{3} \Big|_{0}^{1-x} = \frac{(1-x)^3}{3} $$
So, combining these gives:
$$ x^2(1-x) + \frac{(1-x)^3}{3} $$
- Integrate with Respect to $x$
Now substitute the result from the previous step into the outer integral:
$$ \int_{0}^{1} \left( x^2(1-x) + \frac{(1-x)^3}{3} \right) , dx $$
This can be evaluated as two separate integrals:
$$ \int_{0}^{1} x^2(1-x) , dx + \frac{1}{3} \int_{0}^{1} (1-x)^3 , dx $$
- Evaluate Each Integral
The first integral is:
$$ \int_{0}^{1} x^2(1-x) , dx = \int_{0}^{1} (x^2 - x^3) , dx = \left[ \frac{x^3}{3} - \frac{x^4}{4} \right]_{0}^{1} = \frac{1}{3} - \frac{1}{4} = \frac{1}{12} $$
The second integral simplifies to:
$$ \int_{0}^{1} (1-x)^3 , dx = \frac{1}{4} $$
Therefore:
$$ \frac{1}{3} \cdot \frac{1}{4} = \frac{1}{12} $$
- Combine the Results
Now, sum these results from the two integrals:
$$ \frac{1}{12} + \frac{1}{12} = \frac{1}{6} $$
The final answer is:
$$ \frac{1}{6} $$
More Information
This result represents the average value of the function $f(x, y) = x^2 + y^2$ over the specified triangular region. The integration effectively finds the area under the surface defined by the function over that region.
Tips
- Confusing the limits of integration: Make sure to properly identify the limits based on the triangular area.
- Forgetting to separate the double integral correctly: It’s important to handle the inner and outer integrals distinctly.
AI-generated content may contain errors. Please verify critical information