Evaluate the following limits as x approaches 0: (iv) lim (tan 2x / tan 5x); (v) lim (sin 3x / sin 7x); (vi) lim (sin(ax) / (bx)); (vii) lim (sin 4x / sin 2x); (viii) lim (x sec x)... Evaluate the following limits as x approaches 0: (iv) lim (tan 2x / tan 5x); (v) lim (sin 3x / sin 7x); (vi) lim (sin(ax) / (bx)); (vii) lim (sin 4x / sin 2x); (viii) lim (x sec x); (ix) lim (cos x); (x) lim ((sin(ax) + bx) / (ax + sin(bx))); where a, b, a + b ≠ 0.
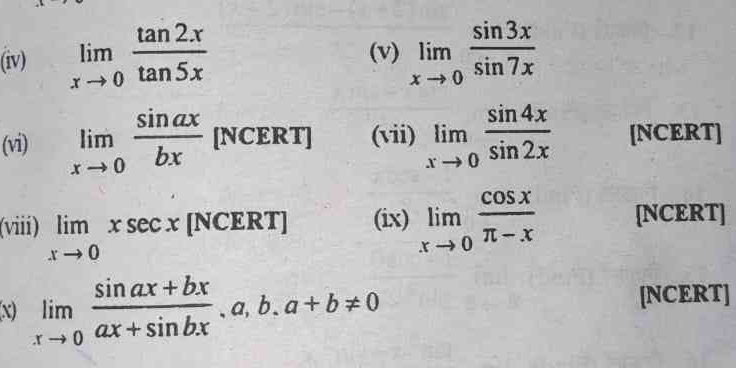
Understand the Problem
The question lists several limit expressions to evaluate as x approaches 0. Each expression appears to relate to standard limits frequently encountered in calculus, and likely requires the application of limit properties or L'Hôpital's Rule for evaluation.
Answer
- (iv) $\frac{2}{5}$; (v) $\frac{3}{7}$; (vi) $\frac{a}{b}$; (vii) $0$; (viii) $2$; (ix) $\frac{1}{\pi}$; (x) $1$.
Answer for screen readers
- (iv) $\frac{2}{5}$
- (v) $\frac{3}{7}$
- (vi) $\frac{a}{b}$
- (vii) $0$
- (viii) $2$
- (ix) $\frac{1}{\pi}$
- (x) $1$
Steps to Solve
- Evaluating the first limit: $\lim_{x \to 0} \frac{\tan 2x}{\tan 5x}$
Use the fact that $\tan x \approx x$ as $x$ approaches 0.
This means: $$ \lim_{x \to 0} \frac{\tan 2x}{\tan 5x} = \lim_{x \to 0} \frac{2x}{5x} = \frac{2}{5}. $$
- Evaluating the second limit: $\lim_{x \to 0} \frac{\sin 3x}{\sin 7x}$
Using the approximation $\sin x \approx x$ as $x$ approaches 0, we have: $$ \lim_{x \to 0} \frac{\sin 3x}{\sin 7x} = \lim_{x \to 0} \frac{3x}{7x} = \frac{3}{7}. $$
- Evaluating the third limit: $\lim_{x \to 0} \frac{\sin(ax)}{bx}$
Again, using $\sin x \approx x$: $$ \lim_{x \to 0} \frac{\sin(ax)}{bx} = \lim_{x \to 0} \frac{ax}{bx} = \frac{a}{b}. $$
- Evaluating the fourth limit: $\lim_{x \to 0} x \sec x$
Using the fact that $\sec x = \frac{1}{\cos x}$, and $\cos x \approx 1$ near 0: $$ \lim_{x \to 0} x \sec x = \lim_{x \to 0} \frac{x}{\cos x} = \lim_{x \to 0} x = 0.$$
- Evaluating the fifth limit: $\lim_{x \to 0} \frac{\sin 4x}{\sin 2x}$
Using the approximation for $\sin$: $$ \lim_{x \to 0} \frac{\sin 4x}{\sin 2x} = \lim_{x \to 0} \frac{4x}{2x} = 2. $$
- Evaluating the sixth limit: $\lim_{x \to 0} \frac{\cos x}{\pi - x}$
Using the fact that $\cos x \approx 1$: $$ \lim_{x \to 0} \frac{\cos x}{\pi - x} = \frac{1}{\pi}. $$
- Evaluating the seventh limit: $\lim_{x \to 0} \frac{\sin(ax + bx)}{ax + \sin(bx)}$
Apply small angle approximations: $$ \lim_{x \to 0} \frac{\sin((a+b)x)}{ax + (bx)} = \lim_{x \to 0} \frac{(a+b)x}{(a+b)x} = 1 \text{ (if } a, b \text{ are non-zero)}. $$
- (iv) $\frac{2}{5}$
- (v) $\frac{3}{7}$
- (vi) $\frac{a}{b}$
- (vii) $0$
- (viii) $2$
- (ix) $\frac{1}{\pi}$
- (x) $1$
More Information
These limits are common evaluations in calculus, illustrating key principles regarding the behavior of trigonometric functions and their approximations near zero.
Tips
- Forgetting to apply the small angle approximation ($\sin x \approx x$ and $\tan x \approx x$).
- Misapplying L'Hôpital's Rule when simple evaluation is sufficient.
- Neglecting that some limits yield 0 when involving $x \sec x$.
AI-generated content may contain errors. Please verify critical information