Evaluate the following limits: 1. $\lim_{x \to +\infty} \sin^{-1}(\frac{1}{5^x})$ 2. $\lim_{x \to \pi^{-}} \tanh^{-1}(\cos x)$ 3. $\lim_{x \to -\infty} \sin^{-1}(2 + \coth x)$
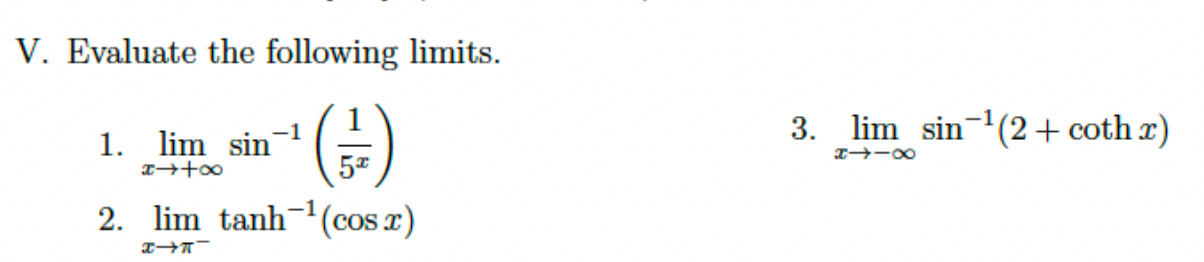
Understand the Problem
The question asks to evaluate several limits involving inverse trigonometric and hyperbolic functions. Specifically, we need to find the limit of (\sin^{-1}(\frac{1}{5^x})) as (x) approaches positive infinity, the limit of (\tanh^{-1}(\cos x)) as (x) approaches (\pi) from the left, and the limit of (\sin^{-1}(2 + \coth x)) as (x) approaches negative infinity.
Answer
1. $\lim_{x \to +\infty} \sin^{-1}(\frac{1}{5^x}) = 0$ 2. $\lim_{x \to \pi^{-}} \tanh^{-1}(\cos x) = -\infty$ 3. $\lim_{x \to -\infty} \sin^{-1}(2 + \coth x) = \frac{\pi}{2}$
Answer for screen readers
- $\lim_{x \to +\infty} \sin^{-1}(\frac{1}{5^x}) = 0$
- $\lim_{x \to \pi^{-}} \tanh^{-1}(\cos x) = -\infty$
- $\lim_{x \to -\infty} \sin^{-1}(2 + \coth x) = \frac{\pi}{2}$
Steps to Solve
-
Evaluate the first limit We need to evaluate $\lim_{x \to +\infty} \sin^{-1}(\frac{1}{5^x})$. As $x$ approaches infinity, $5^x$ also approaches infinity. Thus, $\frac{1}{5^x}$ approaches 0. Since $\sin^{-1}(x)$ is continuous at $x = 0$, we can evaluate the limit by direct substitution: $$ \lim_{x \to +\infty} \sin^{-1}\left(\frac{1}{5^x}\right) = \sin^{-1}\left(\lim_{x \to +\infty} \frac{1}{5^x}\right) = \sin^{-1}(0) = 0 $$
-
Evaluate the second limit We need to evaluate $\lim_{x \to \pi^{-}} \tanh^{-1}(\cos x)$. As $x$ approaches $\pi$ from the left, $\cos x$ approaches $-1$. Since $\tanh^{-1}(x)$ is continuous on its domain $(-1, 1)$, we can evaluate the limit by direct substitution: $$ \lim_{x \to \pi^{-}} \tanh^{-1}(\cos x) = \tanh^{-1}\left(\lim_{x \to \pi^{-}} \cos x\right) = \tanh^{-1}(-1) $$ However, $\tanh^{-1}(-1)$ is not defined, as the domain of $\tanh^{-1}(x)$ is $(-1, 1)$. As $x$ approaches $\pi$ from left, $\cos x$ approaches $-1$ from values greater than $-1$. Thus, $\cos x \to -1^+$. Therefore, $\lim_{x \to \pi^{-}} \tanh^{-1}(\cos x) = -\infty$.
-
Evaluate the third limit We need to evaluate $\lim_{x \to -\infty} \sin^{-1}(2 + \coth x)$. As $x$ approaches $-\infty$, $\coth x$ approaches $-1$. Since $\sin^{-1}(x)$ is continuous, we have: $$ \lim_{x \to -\infty} \sin^{-1}(2 + \coth x) = \sin^{-1}\left(\lim_{x \to -\infty} (2 + \coth x)\right) = \sin^{-1}(2 + (-1)) = \sin^{-1}(1) = \frac{\pi}{2} $$
- $\lim_{x \to +\infty} \sin^{-1}(\frac{1}{5^x}) = 0$
- $\lim_{x \to \pi^{-}} \tanh^{-1}(\cos x) = -\infty$
- $\lim_{x \to -\infty} \sin^{-1}(2 + \coth x) = \frac{\pi}{2}$
More Information
- $\sin^{-1}(x)$ is the inverse sine function, also known as arcsin(x), and its range is $[-\frac{\pi}{2}, \frac{\pi}{2}]$.
- $\tanh^{-1}(x)$ is the inverse hyperbolic tangent function, and its range is $(-\infty, \infty)$ for the domain $(-1, 1)$.
- $\coth(x)$ is the hyperbolic cotangent function, defined as $\coth(x) = \frac{\cosh(x)}{\sinh(x)} = \frac{e^x + e^{-x}}{e^x - e^{-x}}$.
Tips
- Forgetting the domain and range of inverse trigonometric and hyperbolic functions. For example, $\tanh^{-1}(x)$ is only defined for $|x| < 1$.
- Incorrectly evaluating limits of hyperbolic functions. In particular, $\lim_{x \to -\infty} \coth(x) = -1$.
- Not recognizing that as $x \to \pi^-$, $\cos x \to -1^+$, since $\cos x$ values approaches $-1$ from the right along the x-axis.
AI-generated content may contain errors. Please verify critical information