Evaluate the expression given in the attached image.
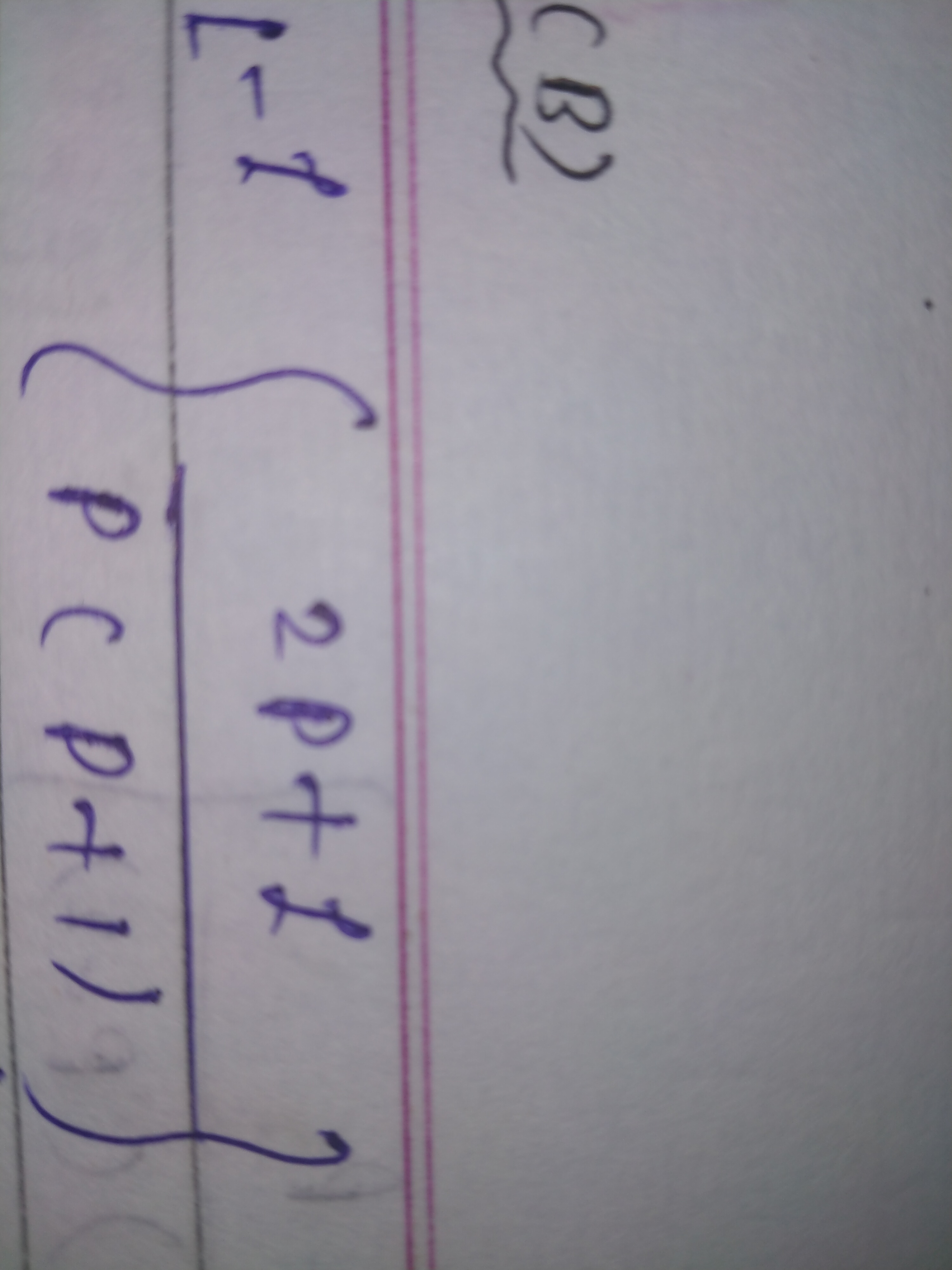
Understand the Problem
The question seems to present a mathematical expression involving a variable. The high-level approach to solving this would include simplifying or solving the equation based on its context.
Answer
The final expression is \( L = p^2 + p - 14pt - 7 \).
Answer for screen readers
The simplified expression is
[ L = p^2 + p - 14pt - 7 ]
Steps to Solve
- Distribute the -7 First, distribute the -7 across the term ( (2pt + 1) ).
[ L = -7(2pt + 1) + p(p + 1) ]
This results in:
[ L = -14pt - 7 + p(p + 1) ]
- Expand ( p(p + 1) ) Next, expand the expression ( p(p + 1) ).
[ p(p + 1) = p^2 + p ]
So now we have:
[ L = -14pt - 7 + p^2 + p ]
- Combine like terms Now, combine all the terms together to form a single expression.
[ L = p^2 + p - 14pt - 7 ]
The simplified expression is
[ L = p^2 + p - 14pt - 7 ]
More Information
This expression is now in a form where we can easily analyze or evaluate it for specific values of ( p ) and ( t ).
Tips
- Forgetting to distribute the negative sign correctly when expanding.
- Not expanding the polynomial ( p(p + 1) ) properly, which leads to incorrect results.
AI-generated content may contain errors. Please verify critical information