Evaluate the definite integral: $\int_{-3}^{3} e^{x^2+1} \cdot \sin^5(x) dx$
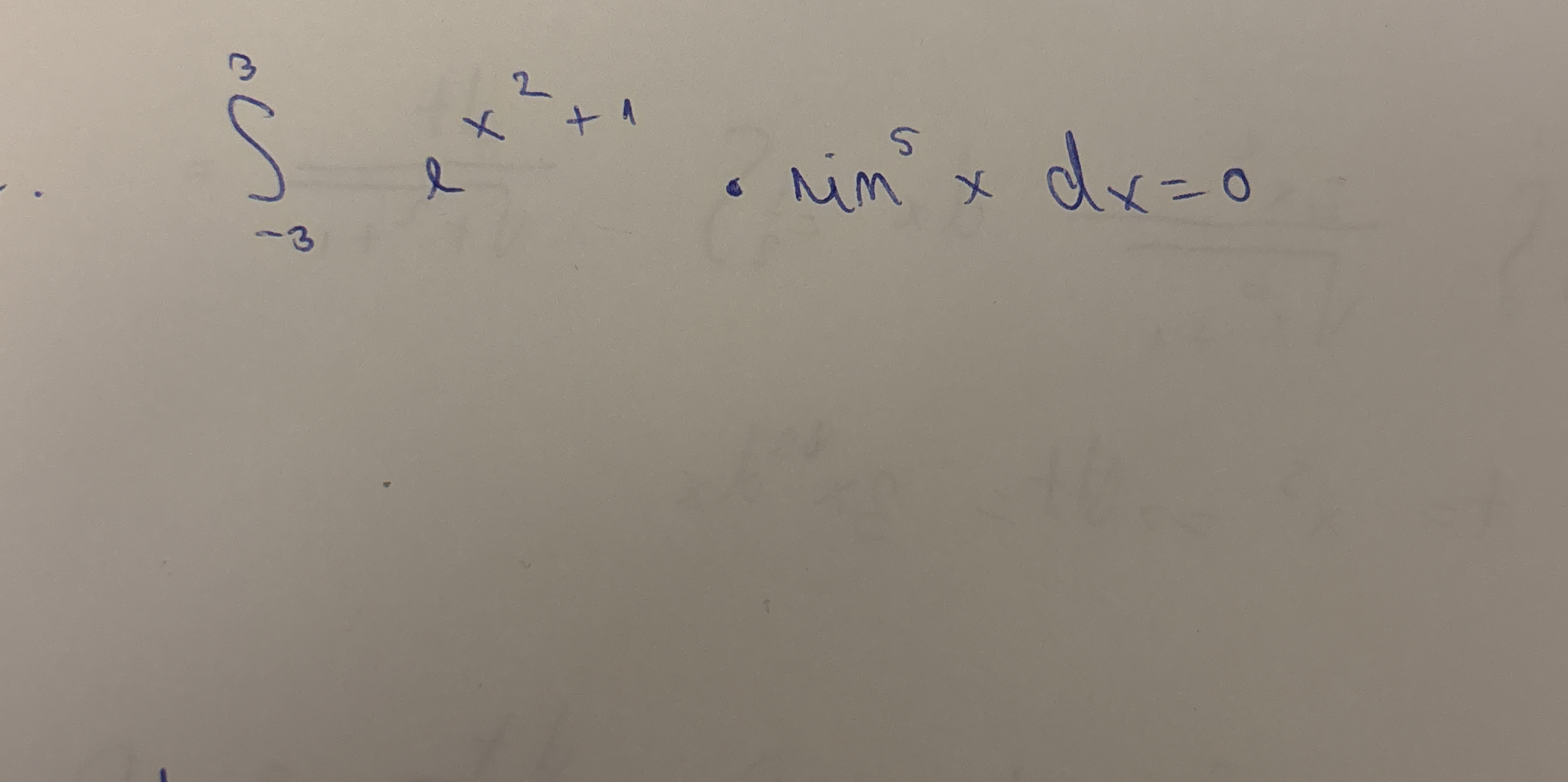
Understand the Problem
The question asks to evaluate a definite integral. The integral involves the product of $e^{x^2+1}$ and $\sin^5(x)$ from -3 to 3. We will need to apply techniques of calculus to solve this problem, paying attention to any symmetry or special properties of the functions involved.
Answer
0
Answer for screen readers
0
Steps to Solve
-
Identify the even and odd functions. $e^{x^2+1}$ is an even function because $e^{(-x)^2+1} = e^{x^2+1}$. $\sin^5(x)$ is an odd function because $\sin^5(-x) = (\sin(-x))^5 = (-\sin(x))^5 = -\sin^5(x)$.
-
Determine the parity of the product. The product of an even and an odd function is an odd function. Therefore, $e^{x^2+1} \cdot \sin^5(x)$ is an odd function.
-
Apply the property of definite integrals of odd functions over symmetric intervals. The definite integral of an odd function over a symmetric interval $[-a, a]$ is zero. In other words, if $f(x)$ is an odd function, then $\int_{-a}^{a} f(x) dx = 0$.
-
Conclude the result. Since $e^{x^2+1} \cdot \sin^5(x)$ is an odd function and the interval of integration is $[-3, 3]$, the integral is zero. $$ \int_{-3}^{3} e^{x^2+1} \cdot \sin^5(x) dx = 0 $$
0
More Information
The integral is zero because we are integrating an odd function over a symmetric interval.
Tips
A common mistake is to try to find the antiderivative of the function, which can be very difficult or impossible. Recognizing the symmetry properties significantly simplifies the problem.
AI-generated content may contain errors. Please verify critical information