Evaluate the definite integral from 0 to pi/2 of the function sin(x)cos(x) / (4 - sin^2(x)) dx.
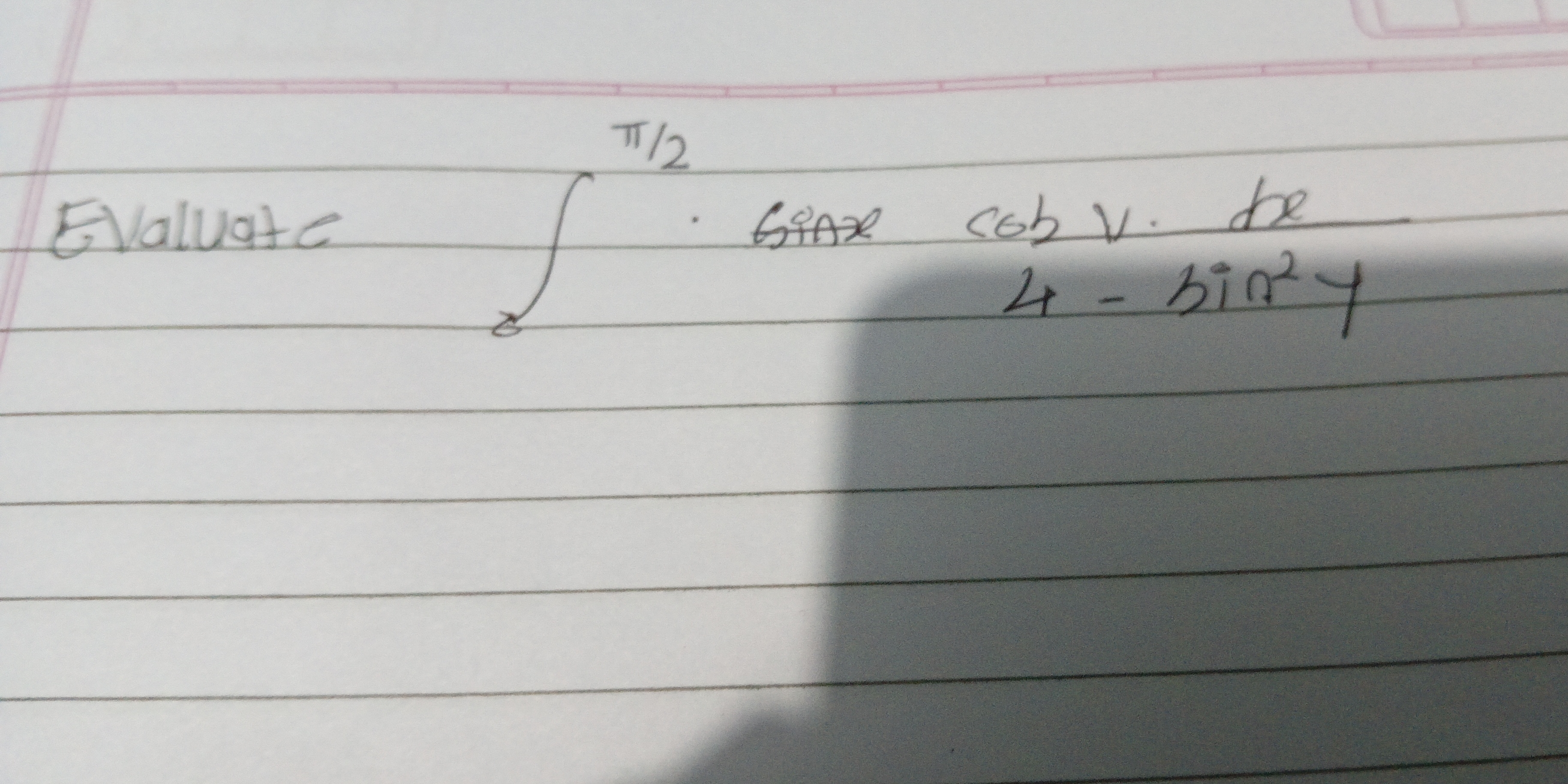
Understand the Problem
The question is asking to evaluate a definite integral from 0 to pi/2 of the function sin(x)cos(x) / (4 - sin^2(x)) dx. We will need to apply appropriate integration techniques to find the solution.
Answer
$\ln(\frac{2}{\sqrt{3}})$
Answer for screen readers
$\ln(\frac{2}{\sqrt{3}})$
Steps to Solve
- Perform u-substitution
Let $u = 4 - \sin^2(x)$. Then, $du = -2\sin(x)\cos(x) dx$. So we have $\sin(x)\cos(x) dx = -\frac{1}{2}du$
- Change the limits of integration
When $x = 0$, $u = 4 - \sin^2(0) = 4 - 0 = 4$. When $x = \frac{\pi}{2}$, $u = 4 - \sin^2(\frac{\pi}{2}) = 4 - 1 = 3$.
- Rewrite the integral
The integral becomes $\int_{4}^{3} \frac{-\frac{1}{2}}{u} du = -\frac{1}{2} \int_{4}^{3} \frac{1}{u} du$
- Evaluate the integral
$-\frac{1}{2} \int_{4}^{3} \frac{1}{u} du = -\frac{1}{2} [\ln|u|]_{4}^{3} = -\frac{1}{2} (\ln(3) - \ln(4)) = -\frac{1}{2} \ln(\frac{3}{4}) = \frac{1}{2} \ln(\frac{4}{3})$
- Simplify the result
Using properties of logarithms, $\frac{1}{2} \ln(\frac{4}{3}) = \ln(\sqrt{\frac{4}{3}}) = \ln(\frac{2}{\sqrt{3}})$
$\ln(\frac{2}{\sqrt{3}})$
More Information
The definite integral of $\frac{\sin(x)\cos(x)}{4 - \sin^2(x)}$ from $0$ to $\frac{\pi}{2}$ is $\ln(\frac{2}{\sqrt{3}})$. This can also be written as $\frac{1}{2} \ln(\frac{4}{3})$.
Tips
A common mistake is forgetting to change the limits of integration when performing u-substitution with definite integrals. Another common mistake is not multiplying by the Jacobian determinant when performing u-substitution
AI-generated content may contain errors. Please verify critical information