Evaluate: lim (x -> 3) (x² + 3)
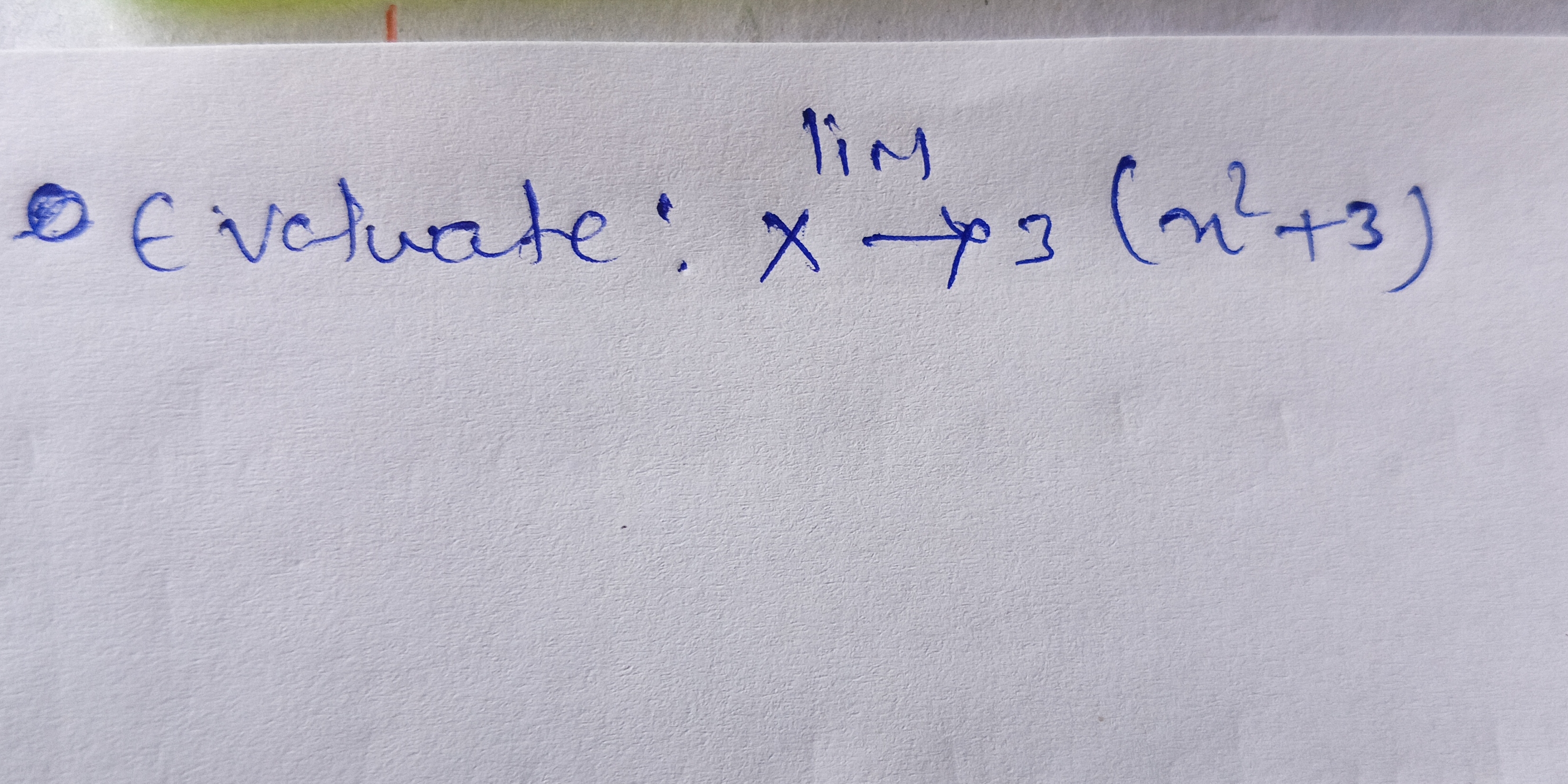
Understand the Problem
The question is asking to evaluate the limit of the expression as x approaches 3. The expression given is (x² + 3).
Answer
The limit is \( 12 \).
Answer for screen readers
The limit is ( 12 ).
Steps to Solve
- Substituting the limit value into the expression
To evaluate the limit as ( x ) approaches 3 for the expression ( x^2 + 3 ), we substitute ( x = 3 ) into the expression:
$$ 3^2 + 3 $$
- Calculating the expression
Next, we calculate the value of the expression:
$$ 3^2 = 9 $$
So, adding 3 gives:
$$ 9 + 3 = 12 $$
- Final result of the limit
Thus, the limit of the expression as ( x ) approaches 3 is:
$$ \lim_{x \to 3} (x^2 + 3) = 12 $$
The limit is ( 12 ).
More Information
The limit evaluates the value of a function as the input gets arbitrarily close to a specified value. In this case, substituting directly into the function yielded a straightforward result.
Tips
- Mistaking the operation order: Ensure to perform exponentiation before addition.
- Forgetting to substitute the limit point correctly.
AI-generated content may contain errors. Please verify critical information