Evaluate ∫ dx / (a^2 - x^2)^(3/2)

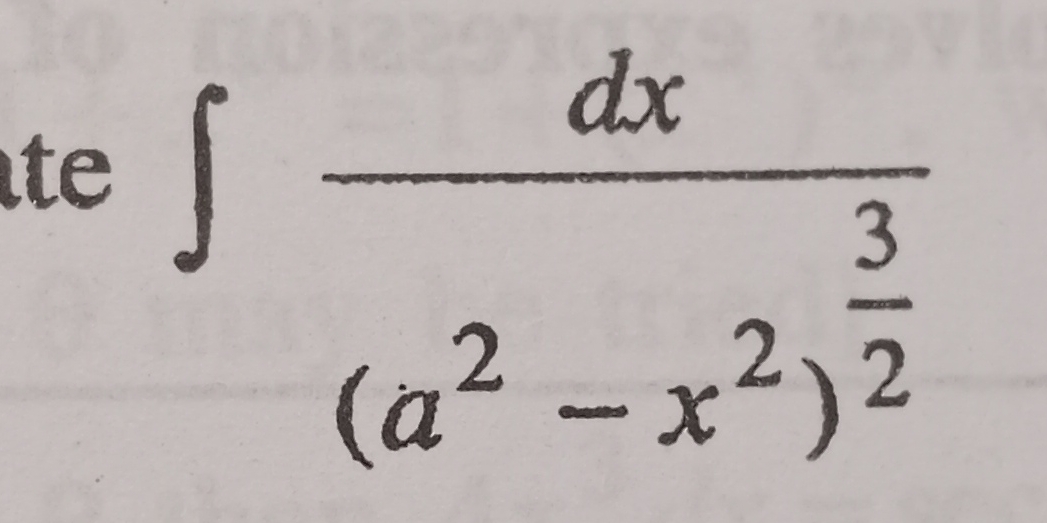
Understand the Problem

The question is asking for the evaluation of the integral of the given expression involving x and a, specifically the integral of dx divided by the square root of (a squared minus x squared) raised to the power of 3/2.

Answer

$$ \int \frac{dx}{(a^2 - x^2)^{3/2}} = \frac{1}{a^2} \frac{x}{\sqrt{a^2 - x^2}} + C $$

Steps to Solve

Identify the Integral

We have the integral

$$ \int \frac{dx}{(a^2 - x^2)^{3/2}} $$
Use the Substitution Method

Let’s set

$$ x = a \sin(\theta) $$

Then,

$$ dx = a \cos(\theta) d\theta $$

and

$$ a^2 - x^2 = a^2(1 - \sin^2(\theta)) = a^2 \cos^2(\theta) $$
Rewrite the Integral

Substitute into the integral,

$$ \int \frac{a \cos(\theta) d\theta}{(a^2 \cos^2(\theta))^{3/2}} = \int \frac{a \cos(\theta) d\theta}{a^3 \cos^3(\theta)} $$

This simplifies to

$$ \int \frac{d\theta}{a^2 \cos^2(\theta)} $$
Simplify the Integral

Recognizing $ \sec(\theta) = \frac{1}{\cos(\theta)} $, we have:

$$ \int \sec^2(\theta) \frac{d\theta}{a^2} $$

This evaluates to

$$ \frac{1}{a^2} \tan(\theta) + C $$
Re-substitute the Original Variable

Recall that

$$ \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} = \frac{x/a}{\sqrt{1 - \sin^2(\theta)}} = \frac{x/a}{\sqrt{(a^2 - x^2)/a^2}} = \frac{x}{\sqrt{a^2 - x^2}} $$

So, we have:

$$ \int \frac{dx}{(a^2 - x^2)^{3/2}} = \frac{1}{a^2} \frac{x}{\sqrt{a^2 - x^2}} + C $$

$$ \int \frac{dx}{(a^2 - x^2)^{3/2}} = \frac{1}{a^2} \frac{x}{\sqrt{a^2 - x^2}} + C $$

More Information

This result shows how using a trigonometric substitution can simplify the process of integrating functions involving square roots, particularly in the context of calculus.

Tips

Forgetting the substitution for (dx) when substituting trigonometric identities.
Not correctly simplifying terms in the integral after substitution.
Overlooking the need to convert back from (\theta) to (x) at the end.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!