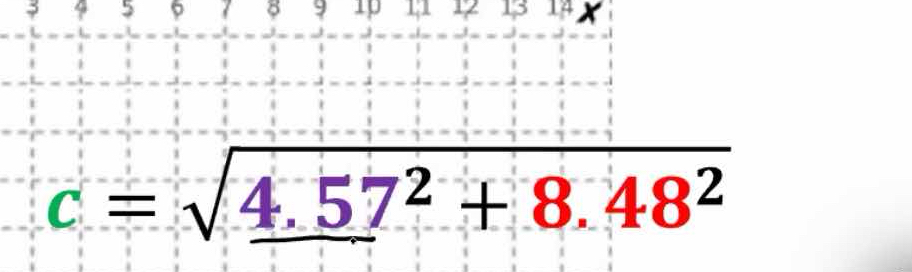
Evaluate $c = \sqrt{4.57^2 + 8.48^2}$
Understand the Problem
The question asks to evaluate the expression c=√(4.57²+8.48²). This involves squaring two numbers, adding the results, and then taking the square root of the sum.
Answer
$c \approx 9.6329$
Answer for screen readers
$c \approx 9.6329$
Steps to Solve
- Calculate $4.57^2$
Square the number $4.57$.
$4.57^2 = 4.57 \times 4.57 = 20.8849$
- Calculate $8.48^2$
Square the number $8.48$.
$8.48^2 = 8.48 \times 8.48 = 71.9104$
- Add the results
Add the results from the previous two steps:
$20.8849 + 71.9104 = 92.7953$
- Take the square root
Take the square root of the sum we found above:
$\sqrt{92.7953} \approx 9.6329$
$c \approx 9.6329$
More Information
The value of $c$ is approximately $9.6329$. This type of calculation is often used in geometry when finding the length of the hypotenuse of a right triangle using the Pythagorean theorem where $a$ and $b$ are the lengths of the two shorter sides, and $c$ is the length of the hypotenuse: $c = \sqrt{a^2 + b^2}$.
Tips
A common mistake is to calculate the square root of each number individually before adding them. Remember that $\sqrt{a^2 + b^2}$ is not equal to $a + b$. You must square each number, then add them, and then take the square root of the sum.
AI-generated content may contain errors. Please verify critical information