Evaluate $4^{-3}$ without an exponent.
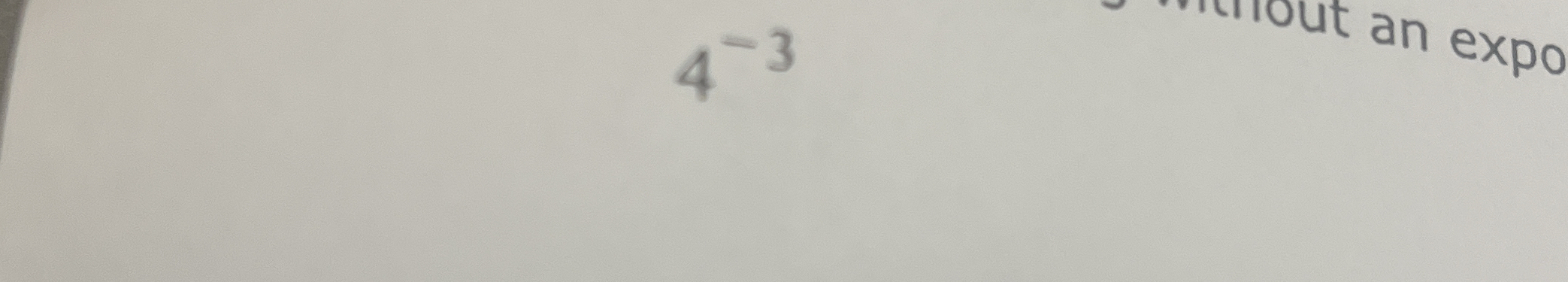
Understand the Problem
The question asks to evaluate the expression $4^{-3}$ and express the result without an exponent.
Answer
$\frac{1}{64}$
Answer for screen readers
$\frac{1}{64}$
Steps to Solve
-
Rewrite the expression with a positive exponent The negative exponent indicates we should take the reciprocal of the base raised to the positive exponent: $4^{-3} = \frac{1}{4^3}$
-
Expand the exponent $4^3$ means $4$ multiplied by itself three times. $\frac{1}{4^3} = \frac{1}{4 \cdot 4 \cdot 4}$
-
Calculate the product in the denominator Multiply the numbers in the denominator: $\frac{1}{4 \cdot 4 \cdot 4} = \frac{1}{16 \cdot 4} = \frac{1}{64}$
$\frac{1}{64}$
More Information
$4^{-3}$ is equivalent to $\frac{1}{4^3}$, which is equal to $\frac{1}{64}$.
Tips
A common mistake is to think that a negative exponent makes the number negative. Instead, a negative exponent means you take the reciprocal of the base raised to the positive value of that exponent. For example, $x^{-n} = \frac{1}{x^n}$, not $-x^n$.
AI-generated content may contain errors. Please verify critical information