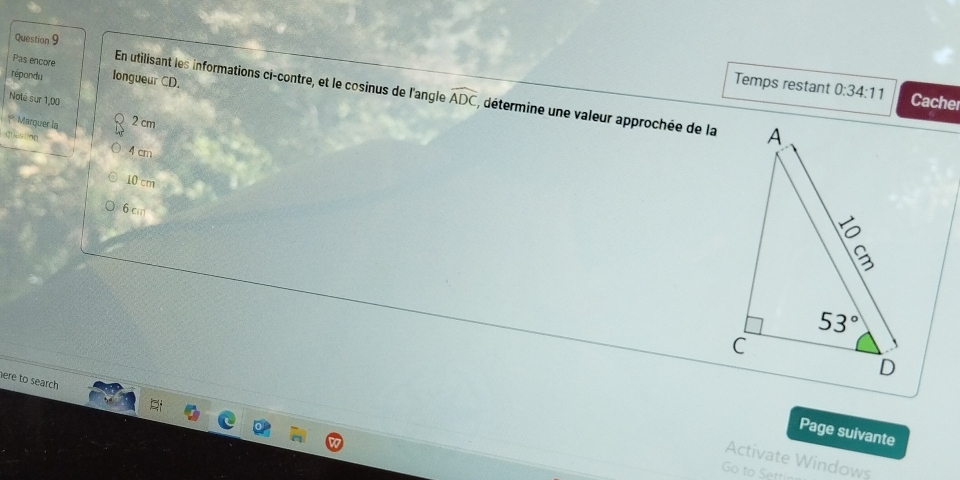
En utilisant les informations ci-contre, et le cosinus de l'angle ADC, détermine une valeur approchée de la longueur CD.
Understand the Problem
La question demande de déterminer la valeur approchée de la longueur CD dans un triangle, en utilisant les informations données, notamment le cosinus de l'angle ADC.
Answer
La longueur CD est approximativement $6.02 \, \text{cm}$.
Answer for screen readers
La valeur approchée de la longueur CD est $6.018 , \text{cm}$.
Steps to Solve
- Identifier les données du triangle
Dans le triangle ADC, nous avons:
- La longueur AD = 10 cm
- L'angle ADC = 53°
- Utiliser la définition du cosinus
Le cosinus de l'angle ADC peut être exprimé par la formule: $$ \cos(ADC) = \frac{CD}{AD} $$
- Substituer les valeurs connues
En substituant les valeurs dans l'équation: $$ \cos(53°) = \frac{CD}{10} $$
- Calculer le cosinus de 53°
On utilise une calculatrice ou une table de valeurs pour trouver: $$ \cos(53°) \approx 0.6018 $$
- Résoudre pour CD
Substituez le cosinus dans l'équation: $$ 0.6018 = \frac{CD}{10} $$
Pour trouver CD, multipliez des deux côtés par 10: $$ CD = 10 \times 0.6018 $$
- Calcul final
En effectuant le calcul: $$ CD \approx 6.018 , \text{cm} $$
La valeur approchée de la longueur CD est $6.018 , \text{cm}$.
More Information
Le cosinus d'un angle dans un triangle permet de relier un côté du triangle et l'angle. Ainsi, en connaissant un côté et un angle, on peut facilement trouver la longueur d'un autre côté.
Tips
- Confondre le cosinus et le sinus : Assurez-vous d'utiliser la définition appropriée en fonction de l'angle donné.
- Oublier de multiplier par 10 : Certains peuvent négliger le dernier calcul après avoir isolé CD.
AI-generated content may contain errors. Please verify critical information