En la figura, AC // BD, entonces ¿cuánto mide x?
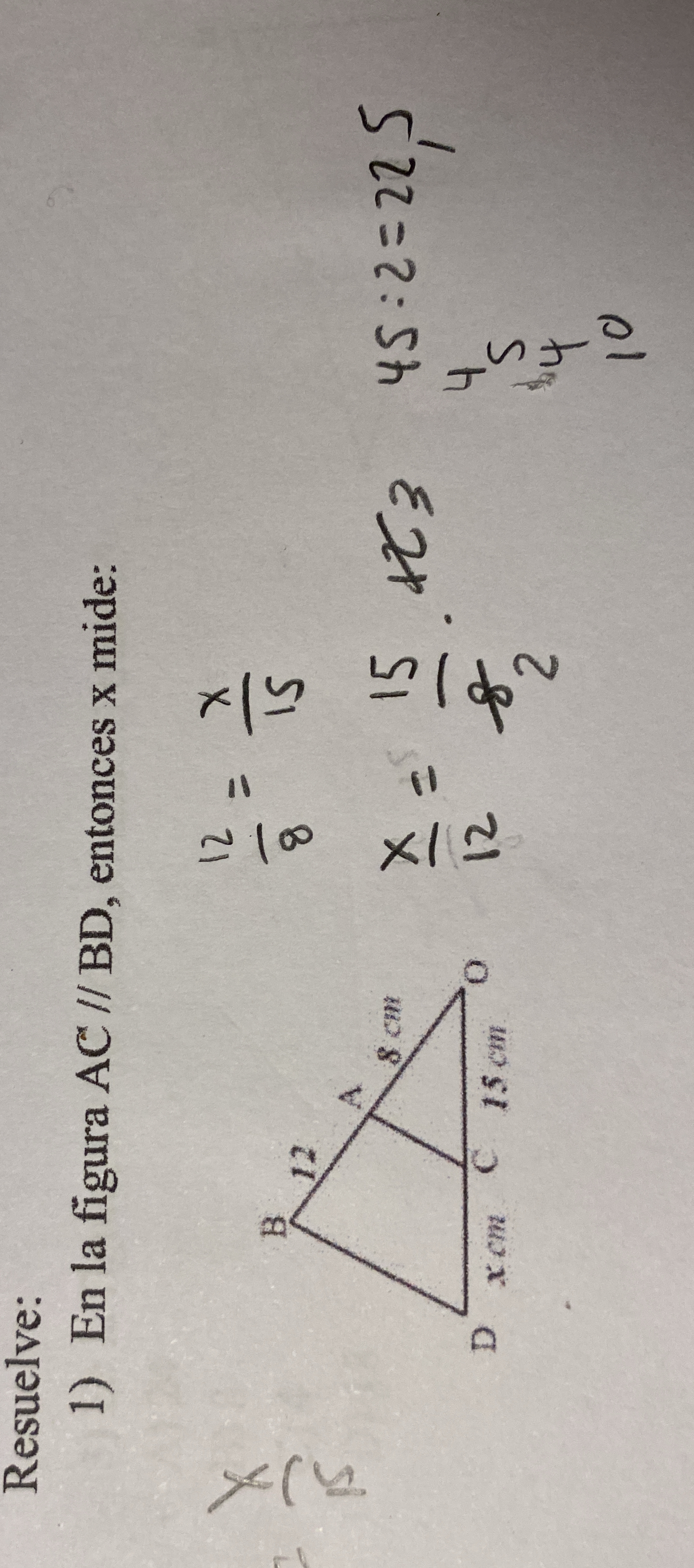
Understand the Problem
El problema presenta una figura geométrica con las líneas AC y BD paralelas. Se pide calcular la longitud 'x' basándose en las proporciones dadas en la figura.
Answer
$x = 22.5$
Answer for screen readers
$x = 22.5$
Steps to Solve
-
Set up the proportion The problem states that $\frac{12}{8} = \frac{x}{15}$.
-
Solve for $x$ To isolate $x$, multiply both sides of the equation by 15: $$ x = 15 \cdot \frac{12}{8} $$
-
Simplify the fraction Simplify the fraction by dividing 12 and 8 by their greatest common divisor, which is 4: $$ x = 15 \cdot \frac{3}{2} $$
-
Calculate $x$ Multiply 15 by $\frac{3}{2}$: $$ x = \frac{45}{2} = 22.5 $$
$x = 22.5$
More Information
In similar triangles, corresponding sides are proportional. This problem uses that property of similar triangles to find the missing length.
Tips
A common mistake is not simplifying the fraction before multiplying. It is also common to make arithmetic errors during the multiplication and division steps.
AI-generated content may contain errors. Please verify critical information