druk b uit in a gegeven a + 4 = 0.4b² * ⁶√b * ³√b
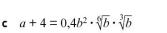
Understand the Problem
De vraag vraagt om b uit te drukken in termen van a. Dit betekent dat we de vergelijking moeten herschrijven zodat b aan één kant van het gelijkteken staat en een uitdrukking met a aan de andere kant.
Answer
$b = (2.5a + 10)^{\frac{2}{5}}$
Answer for screen readers
$b = (2.5a + 10)^{\frac{2}{5}}$
Steps to Solve
- Rewrite the roots as exponents
Rewrite the radicals using fractional exponents:
$ \sqrt[6]{b} = b^{1/6} $ $ \sqrt[3]{b} = b^{1/3} $
The equation becomes: $a + 4 = 0.4b^2 \cdot b^{1/6} \cdot b^{1/3}$
- Combine the $b$ terms on the right side
Use the rule $b^m \cdot b^n = b^{m+n}$ to combine the $b$ terms. To add the exponents, find a common denominator:
$ \frac{1}{6} + \frac{1}{3} = \frac{1}{6} + \frac{2}{6} = \frac{3}{6} = \frac{1}{2} $
So, $ b^{1/6} \cdot b^{1/3} = b^{1/2} $
The equation is now: $ a + 4 = 0.4b^2 \cdot b^{1/2} $
$ a + 4 = 0.4b^{2 + \frac{1}{2}} = 0.4b^{\frac{5}{2}} $
- Isolate the term with $b$
Divide both sides by 0.4:
$ \frac{a + 4}{0.4} = b^{\frac{5}{2}} $
$ 2.5(a + 4) = b^{\frac{5}{2}} $
$ 2.5a + 10 = b^{\frac{5}{2}} $
- Solve for $b$
Raise both sides to the power of $\frac{2}{5}$ to isolate $b$:
$ (2.5a + 10)^{\frac{2}{5}} = (b^{\frac{5}{2}})^{\frac{2}{5}} $
$ (2.5a + 10)^{\frac{2}{5}} = b $
$b = (2.5a + 10)^{\frac{2}{5}}$
More Information
The solution expresses $b$ in terms of $a$. We simplified exponents using fractional powers and combined like terms.
Tips
A common mistake is to incorrectly combine the exponents when multiplying terms with the same base. Always remember to add the exponents, not multiply them! Also, be careful when raising both sides of an equation to a fractional power to isolate the variable; make sure to apply the exponent correctly to both sides.
AI-generated content may contain errors. Please verify critical information