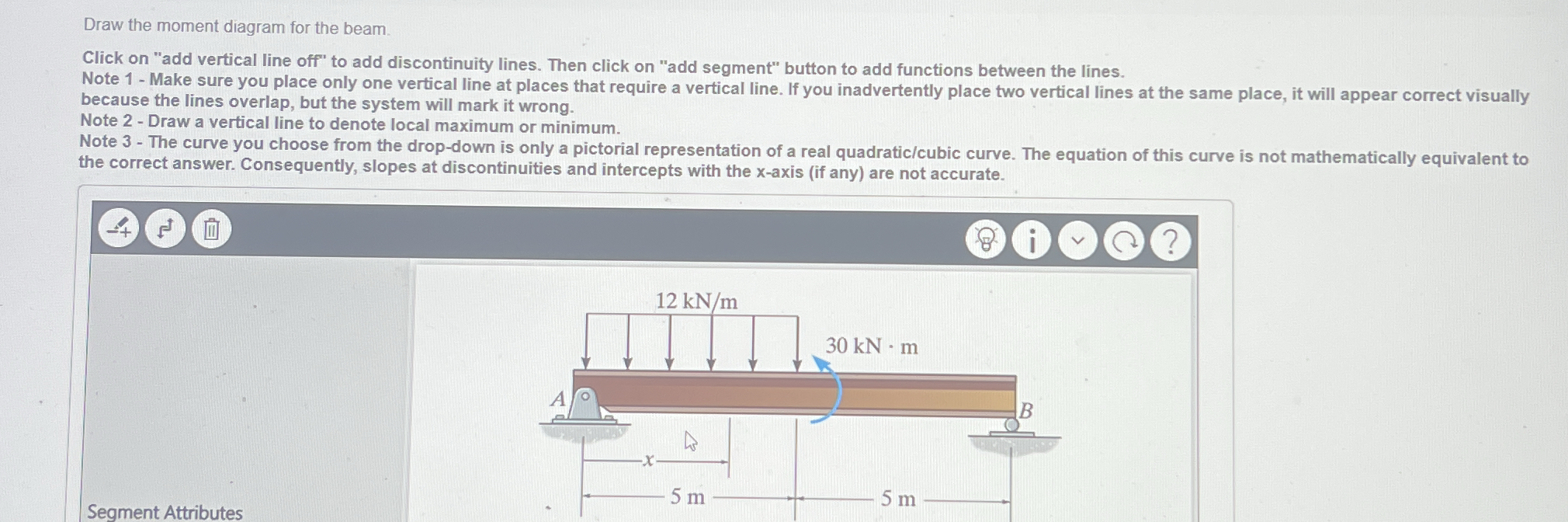
Draw the moment diagram for the beam.

Steps to Solve

1. Calculate the reactions at supports A and B

First, calculate the total downward load from the uniformly distributed load (UDL):

$12 , \text{kN/m} \times 10 , \text{m} = 120 , \text{kN}$

Let $R_A$ and $R_B$ be the vertical reactions at supports A and B, respectively. Take the sum of the moments about point A to solve for $R_B$:

$$ \sum M_A = 0 = R_B \times 10 , \text{m} - 120 , \text{kN} \times 5 , \text{m} + 30 , \text{kN}\cdot\text{m} $$ $$ R_B \times 10 , \text{m} = 600 , \text{kN}\cdot\text{m} - 30 , \text{kN}\cdot\text{m} = 570 , \text{kN}\cdot\text{m} $$ $$ R_B = 57 , \text{kN} $$

Now, take the sum of the forces in the vertical direction to solve for $R_A$:

$$ \sum F_y = 0 = R_A + R_B - 120 , \text{kN} $$ $$ R_A = 120 , \text{kN} - R_B = 120 , \text{kN} - 57 , \text{kN} $$ $$ R_A = 63 , \text{kN} $$

2. Determine the bending moment equation for the first segment (0 ≤ x ≤ 5 m)

Consider a section at a distance $x$ from support A. The bending moment $M(x)$ at this section is given by:

$$ M(x) = R_A \cdot x - \frac{1}{2} \cdot (12 , \text{kN/m}) \cdot x^2 $$ $$ M(x) = 63x - 6x^2 $$

3. Evaluate the bending moment at x = 0 m and x = 5 m

At $x = 0 , \text{m}$:

$$ M(0) = 63(0) - 6(0)^2 = 0 , \text{kN}\cdot\text{m} $$

At $x = 5 , \text{m}$:

$$ M(5) = 63(5) - 6(5)^2 = 315 - 150 = 165 , \text{kN}\cdot\text{m} $$

4. Consider the point moment

At $x = 5 , \text{m}$, the point moment of $30 , \text{kN}\cdot\text{m}$ is applied. This introduces a discontinuity. So, just to the right of $x = 5 , \text{m}$ (but before the next segment):

$M(5^+) = 165 - 30 = 135 \text{ kNm}$

5. Determine the bending moment equation for the second segment (5 m ≤ x ≤ 10 m)

For the second segment, the bending moment $M(x)$ accounting for the point moment is given by (where $x$ is still measured from support A):

$$ M(x) = R_A \cdot x - (12 , \text{kN/m}) \cdot x \cdot \frac{x}{2} -30 $$ $$ M(x) = 63x - 6x^2 - 30 $$

6. Evaluate the bending moment at x = 10 m

At $x = 10 , \text{m}$:

$$ M(10) = 63(10) - 6(10)^2 - 30 = 630 - 600 - 30 = 0 , \text{kN}\cdot\text{m} $$

7. Find the location of the maximum moment in the first segment

To find the location of the maximum moment, set the derivative of $M(x)$ with respect to $x$ equal to zero and solve for $x$:

$$ \frac{dM}{dx} = 63 - 12x = 0 $$ $$ x = \frac{63}{12} = 5.25 , \text{m} $$

However, since this value is outside the range of the first segment (0 to 5m), we need to look at the second segment for where the moment will be maximum. (Note: although the overall maxium may be at the end of the first segment, we need to inspect the second segment too.) Let's take the derivative again, for the second part of the beam:

$$ \frac{dM}{dx} = 63 - 12x = 0 $$ $$ x = \frac{63}{12} = 5.25 , \text{m} $$

Since $x$ is measured from support A, and the second section begins at $x=5$, the location of the max moment is indeed in the second section. We plug this into our equation, $ M(x) = 63x - 6x^2 - 30 $ to find the max value of the moment.

$$ M(5.25) = 63(5.25) - 6(5.25)^2 - 30 = 330.75 - 165.375 - 30 = 135.375 \text{ kNm} $$

8. Draw the moment diagram

• The moment diagram starts at 0 at support A.

• It follows a quadratic curve, reaching $165 , \text{kN}\cdot\text{m}$ just to the left of the point moment (at x=5).

• A vertical discontinuity of $30 , \text{kN}\cdot\text{m}$ occurs (it jumps down $30 , \text{kN}\cdot\text{m}$).

• It continues as a quadratic curve, again, ending at 0 at support B.

• Note that the relative maximum occurs at approximately x = 5.25 m.