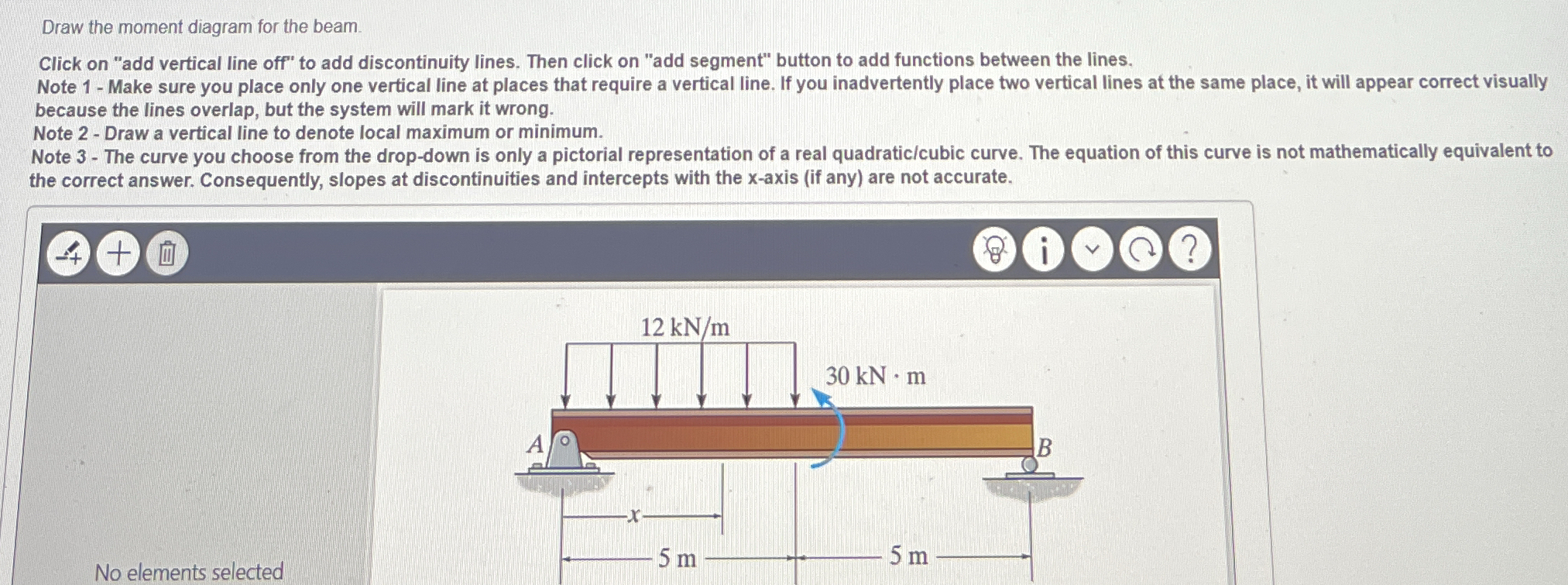
Draw the moment diagram for the beam.

Steps to Solve

1. Calculate the reactions at the supports

Since the structure is symmetric and has a point moment at the center, the reactions at supports A and B will be equal. The total downward force due to the distributed load is $12 \text{ kN/m} \times 5 \text{ m} = 60 \text{ kN}$. Therefore, each support will carry half of that load, plus we need to consider the effect of the moment. Taking the sum of the moments about point A:

$$ \sum M_A = 0 = -30 \text{ kN}\cdot\text{m} - (60 \text{ kN}) (2.5 \text{ m}) + R_B (5 \text{ m}) $$

Solving for $R_B$:

$$ R_B = \frac{30 + 60 \times 2.5}{5} = \frac{30 + 150}{5} = \frac{180}{5} = 36 \text{ kN} $$

Since the reactions must balance the applied load plus the effect of the moment:

$$ R_A + R_B = 60 \text{ kN} $$

$$ R_A = 60 - R_B = 60 - 36 = 24 \text{ kN} $$

2. Determine the moment equation for the first section (0 m $\leq$ x $\leq$ 5 m)

Taking a cut at a distance $x$ from support A:

$M(x) = R_A \cdot x - \frac{1}{2} (12 \text{ kN/m}) x^2 = 24x - 6x^2 $

3. Calculate the moment at x=0 m and x=5 m

$M(0) = 24(0) - 6(0)^2 = 0 \text{ kN}\cdot\text{m}$

$M(5) = 24(5) - 6(5)^2 = 120 - 150 = -30 \text{ kN}\cdot\text{m}$

4. Consider the applied moment

At $x=5$ m, there is a point moment of $30 \text{ kN}\cdot\text{m}$ is applied. Since it is a negative moment (clockwise), this will cancel part of the beam's internal moment.

5. Determine the moment equation for the second section (5 m $\leq$ x $\leq$ 10 m)

Taking a cut at a distance $x$ from support A, and including the effect of the point moment:

Starting from the section at position $x$:

$M(x) = R_A \cdot x - (\text{distributed load}) \cdot (x-2.5) \cdot \frac{x-2.5}{2} - 30 $ for one portion. So

$$ M(x) = 24x - 6x^2$$ Then since we have a point moment at 5m, we will have just that value there i.e. $-30 \text{ kN}\cdot\text{m}$ at $x=5$.

Then, after 5 m to the bearing support B, or $10$ m: $M(10) = 0$

Alternatively, one can consider the moment as a function to be determined by sections of the beam as follows:

For $0 \leq x \leq 5$: $M(x) = 24x - 6x^2$

At $x=5$, we have $M(5) = 24(5) - 6(5^2) = 120 - 150 = -30$. Then, the $30 \text{ kN}\cdot\text{m}$ is applied at 5m and therefore from here we have: $M(x') = -30$. Then since $x' = x-5, \text{ }x = x' + 5$. $M(x)= 36 * (10-x) = 360 - 36x $ Let $x'= 0 , x = 5$. $M(5) = 360 - 36(5) = 360-180 = 180 $ If $M(x)= 6*(10-x)(10-x)$ Let $x'= 0 , x = 5$. $M(5) = 6(5)*(5) = 150 $

6. Final Moment diagram

The moment diagram will start from 0 at support A, follow a quadratic curve down to -30 kN*m just before the applied moment at x=5 m. At x=5 m, there is a jump in the diagram due to the applied moment to 0. Then the diagram follows a linear path to 0 at the support B.