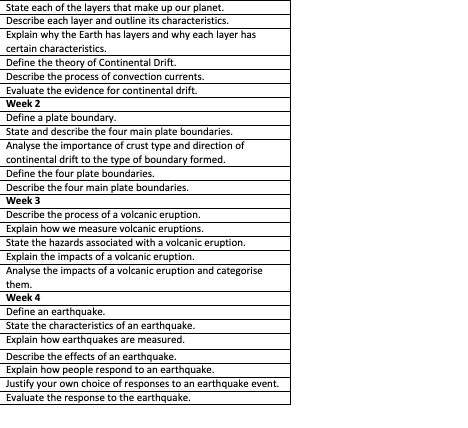
Understand the Problem
The question is seeking assistance with a mathematical problem, specifically related to an image that likely contains a mathematical equation or concept.
Answer
The function is \( y = \frac{1}{x} \) with domain \( x \in \mathbb{R} \setminus \{0\} \) and range \( y \in \mathbb{R} \setminus \{0\} \).
Answer for screen readers
The function is ( y = \frac{1}{x} ), with the following properties:
- Domain: ( x \in \mathbb{R} \setminus {0} )
- Range: ( y \in \mathbb{R} \setminus {0} )
- No intercepts
- Asymptotes at ( x=0 ) and ( y=0 )
Steps to Solve
-
Identify the equation
The equation shown is ( y = \frac{1}{x} ). This is a rational function, which means the output (( y )) is determined by the reciprocal of the input (( x )). -
Determine the characteristics of the function
To analyze this function, we need to study its properties:
- Domain: The values of ( x ) can be any real number except zero, so the domain is ( x \in \mathbb{R} \setminus {0} ).
- Range: The values of ( y ) can also be any real number except zero, giving a range of ( y \in \mathbb{R} \setminus {0} ).
- Calculate intercepts
- Y-intercept: To find the y-intercept, set ( x = 0 ). However, since the function is undefined at ( x = 0 ), there is no y-intercept.
- X-intercept: Set ( y = 0 ). The equation cannot equal zero, thus there are no x-intercepts either.
- Graph the function
Sketch the graph of the function. The graph will have two branches that approach the axes but never touch them (asymptotes):
- Horizontal asymptote at ( y = 0 )
- Vertical asymptote at ( x = 0 )
- Behavior of the function
The function ( y ) approaches ( 0 ) as ( x ) approaches (\pm \infty). As ( x ) approaches ( 0 ) from the right, ( y ) tends to ( +\infty ) and from the left, ( y ) tends to ( -\infty ).
The function is ( y = \frac{1}{x} ), with the following properties:
- Domain: ( x \in \mathbb{R} \setminus {0} )
- Range: ( y \in \mathbb{R} \setminus {0} )
- No intercepts
- Asymptotes at ( x=0 ) and ( y=0 )
More Information
This function is an example of a hyperbola and commonly appears in calculus and various applied mathematics fields. Its properties make it important in understanding limits, asymptotic behavior, and rational functions.
Tips
- Forgetting that the function is undefined at zero, leading to incorrect conclusions about intercepts.
- Confusing the behavior of the function as ( x ) approaches zero; it goes to infinity, not to zero.
AI-generated content may contain errors. Please verify critical information