Divide $4x^2 - 8x + 3$ by $x - 1$ using synthetic division.
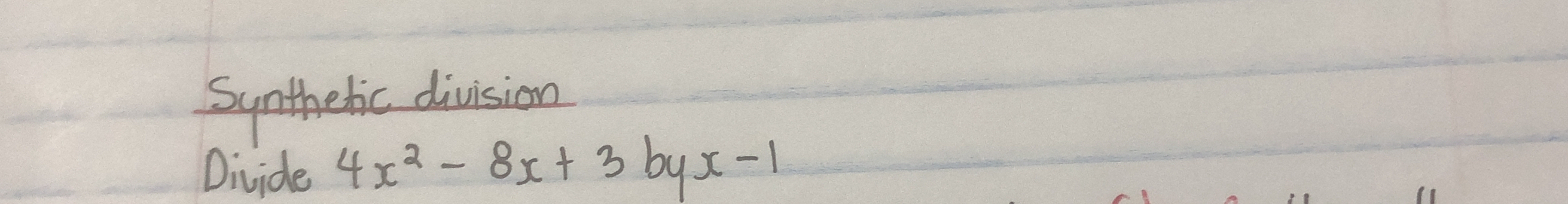
Understand the Problem
The question asks to perform synthetic division of the polynomial $4x^2 - 8x + 3$ by $x - 1$. Synthetic division is a simplified method for dividing a polynomial by a linear factor of the form $x - a$.
Answer
$4x - 4 - \frac{1}{x-1}$
Answer for screen readers
$4x - 4 - \frac{1}{x-1}$
Steps to Solve
- Identify the coefficients and the divisor root
The polynomial is $4x^2 - 8x + 3$, so the coefficients are $4$, $-8$, and $3$. The divisor is $x - 1$, so the root is $1$.
- Set up the synthetic division
Write the root ($1$) to the left and the coefficients ($4$, $-8$, $3$) to the right.
- Bring down the first coefficient
Bring down the first coefficient ($4$) to the bottom row.
- Multiply and add
Multiply the root ($1$) by the number you just brought down ($4$), which gives $4$. Write this under the next coefficient ($-8$). Add $-8$ and $4$ to get $-4$.
- Repeat the process
Multiply the root ($1$) by the result ($-4$), which gives $-4$. Write this under the next coefficient ($3$). Add $3$ and $-4$ to get $-1$.
- Interpret the result
The numbers on the bottom row are the coefficients of the quotient and the remainder. Since we started with a quadratic ($x^2$) and divided by a linear term ($x$), the quotient will be linear ($x$). The last number is the remainder. In this case, the quotient is $4x - 4$ and the remainder is $-1$.
- Write the final answer
The result of the division is the quotient plus the remainder divided by the divisor: $4x - 4 + \frac{-1}{x-1}$.
$4x - 4 - \frac{1}{x-1}$
More Information
Synthetic division provides a shortcut for polynomial division when dividing by a linear factor. The result includes both the quotient and the remainder.
Tips
A common mistake is to forget to include the remainder in the final answer, or to misinterpret the coefficients obtained in the synthetic division process. Another common mistake is getting the sign wrong when determining the root to use in the synthetic division (e.g., using -1 instead of 1 when dividing by $x - 1$).
AI-generated content may contain errors. Please verify critical information