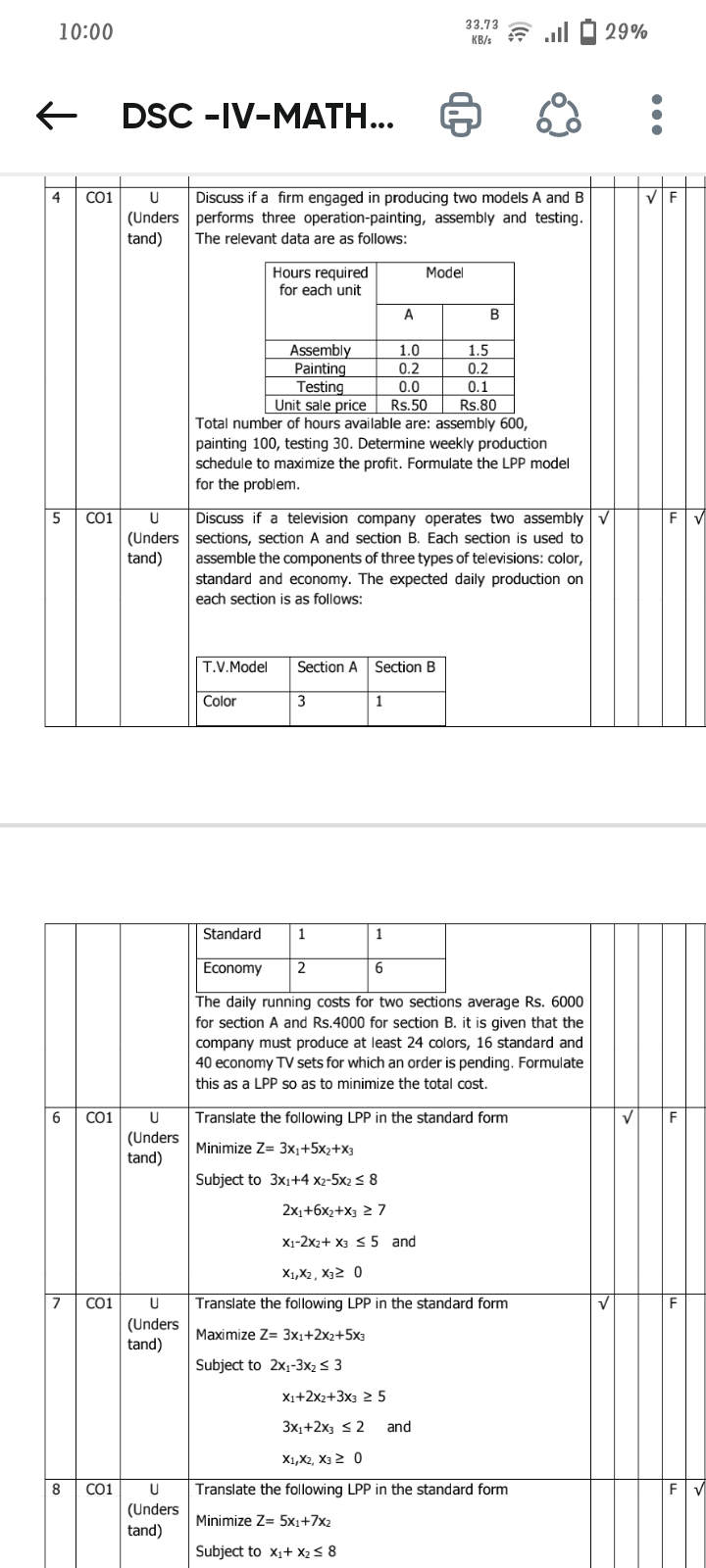
Discuss if a firm engaged in producing two models A and B performs three operations: painting, assembly, and testing. The relevant data are as follows: Hours required for each unit... Discuss if a firm engaged in producing two models A and B performs three operations: painting, assembly, and testing. The relevant data are as follows: Hours required for each unit: Model A: Assembly 1.0, Painting 0.2, Testing 0.0; Model B: Assembly 1.5, Painting 0.2, Testing 0.1. Total hours available: assembly 600, painting 100, testing 30. Determine weekly production schedule to maximize profit. Formulate the LPP model for the problem.
Understand the Problem
The question is asking for the formulation of a linear programming problem (LPP) based on given data for two different production scenarios, aiming to either maximize profit or minimize cost. It involves analyzing constraints related to labor hours and production capabilities.
Answer
Maximize: $Z = 50x_1 + 80x_2$; Subject to: $1.0x_1 + 1.5x_2 \leq 600$, $0.2x_1 + 0.2x_2 \leq 100$, $0.1x_2 \leq 30$, $x_1 \geq 0$, $x_2 \geq 0$.
Answer for screen readers
The LPP model to maximize profit is:
Maximize: $$ Z = 50x_1 + 80x_2 $$
Subject to:
- $$ 1.0x_1 + 1.5x_2 \leq 600 $$
- $$ 0.2x_1 + 0.2x_2 \leq 100 $$
- $$ 0.1x_2 \leq 30 $$
- $$ x_1 \geq 0 $$
- $$ x_2 \geq 0 $$
Steps to Solve
- Define variables for production units
Let:
- $x_1$ = number of units produced for Model A
- $x_2$ = number of units produced for Model B
- Determine the objective function
The profit from each model is calculated as follows:
- Profit from Model A: $50 \cdot x_1$
- Profit from Model B: $80 \cdot x_2$
Thus, the objective function to maximize profit is:
$$ Z = 50x_1 + 80x_2 $$
- Establish constraints based on labor hours
From the problem, the constraints based on the hours available for each activity are:
-
Assembly hours constraint: $$ 1.0x_1 + 1.5x_2 \leq 600 $$
-
Painting hours constraint: $$ 0.2x_1 + 0.2x_2 \leq 100 $$
-
Testing hours constraint: $$ 0.0x_1 + 0.1x_2 \leq 30 $$
- Include non-negativity constraints
The number of units produced cannot be negative:
$$ x_1 \geq 0 $$ $$ x_2 \geq 0 $$
- Compile the complete LPP model
The complete linear programming problem (LPP) can be summarized as follows:
Maximize: $$ Z = 50x_1 + 80x_2 $$
Subject to:
- $$ 1.0x_1 + 1.5x_2 \leq 600 $$
- $$ 0.2x_1 + 0.2x_2 \leq 100 $$
- $$ 0.1x_2 \leq 30 $$
- $$ x_1 \geq 0 $$
- $$ x_2 \geq 0 $$
The LPP model to maximize profit is:
Maximize: $$ Z = 50x_1 + 80x_2 $$
Subject to:
- $$ 1.0x_1 + 1.5x_2 \leq 600 $$
- $$ 0.2x_1 + 0.2x_2 \leq 100 $$
- $$ 0.1x_2 \leq 30 $$
- $$ x_1 \geq 0 $$
- $$ x_2 \geq 0 $$
More Information
This LPP model ensures that the firm optimally uses its limited resources (assembly, painting, and testing hours) to maximize profit while adhering to the constraints of production capacity.
Tips
- Misinterpreting the constraints or incorrectly formulating them can lead to infeasible solutions. Always double-check the required hours against the total available hours.
- Forgetting to include non-negativity constraints is a common oversight that can invalidate the model.
AI-generated content may contain errors. Please verify critical information