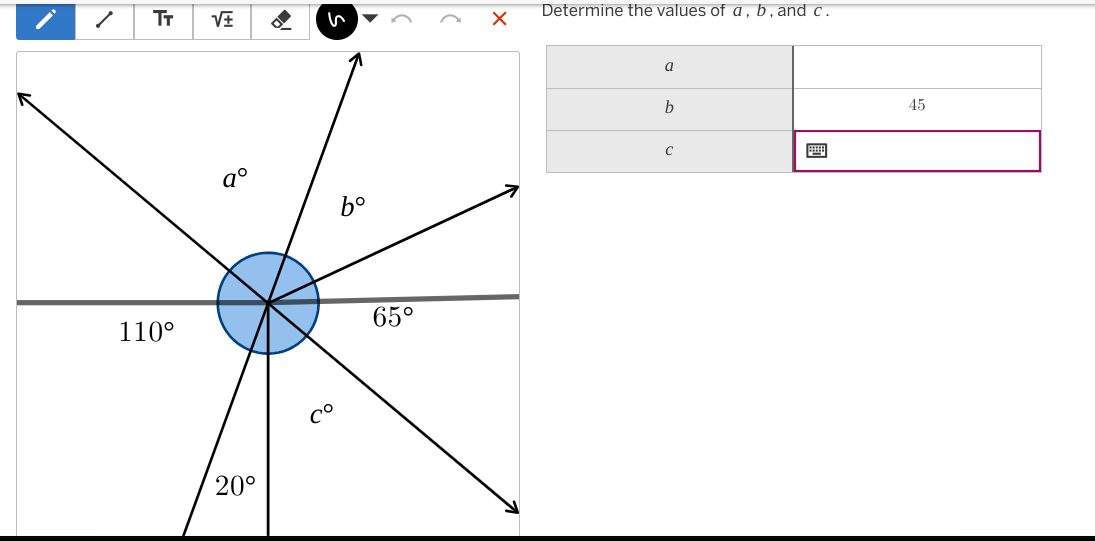
Determine the values of a, b, and c.

Steps to Solve

1. Recognize angles on a straight line Angles on a straight line add up to $180^\circ$. The angles $110^\circ$ and $a^\circ$ form a straight line. Also the angles $65^\circ$ and $b^\circ$ form a straight line.

2. Calculate angle $a$ Since $110^\circ + a = 180^\circ$, we can find $a$ by subtracting $110^\circ$ from $180^\circ$.

$$ a = 180^\circ - 110^\circ = 70^\circ $$

3. Calculate angle $b$ Since $65^\circ + b = 180^\circ$, we can find $b$ by subtracting $65^\circ$ from $180^\circ$.

$$ b = 180^\circ - 65^\circ = 115^\circ $$ However, it is given that $b = 45$, which means the angles indicated with arc are supplementary to 110 and 65. Let's assume that we are looking for angles adjacent to 110 and 65 so we would be consistent. Then we are looking for supplementary angles on the other side so $$ b = 180^\circ - 45^\circ = 135^\circ $$

4. Recognize angles around a point Angles around a point add up to $360^\circ$. Thus, $110^\circ + 20^\circ + 65^\circ + a + b + c = 360^\circ$. Let's assume again that $a$ and $b$ are adjacent angles, and instead are supplementary to 110 and 65.

5. Calculate angle $c$ We know that $a = 70^\circ$ and $b=135^\circ$ and we know the rest of the angles: $110^\circ, 65^\circ, 20^\circ$. Now we can substitute these values into the equation from step 4 and solve for $c$. $$ 70^\circ + 135^\circ + c + 20^\circ + 110^\circ + 65^\circ = 360^\circ $$ $$ 400^\circ + c = 360^\circ $$ $$ c = 360^\circ - 400^\circ = -40^\circ $$ However, we are given $b = 45^\circ$. Let's substitute $b = 45^\circ$. $$ 70^\circ + 45^\circ + c + 20^\circ + 110^\circ + 65^\circ = 360^\circ $$ $$ 310^\circ + c = 360^\circ $$ $$ c = 360^\circ - 310^\circ = 50^\circ $$