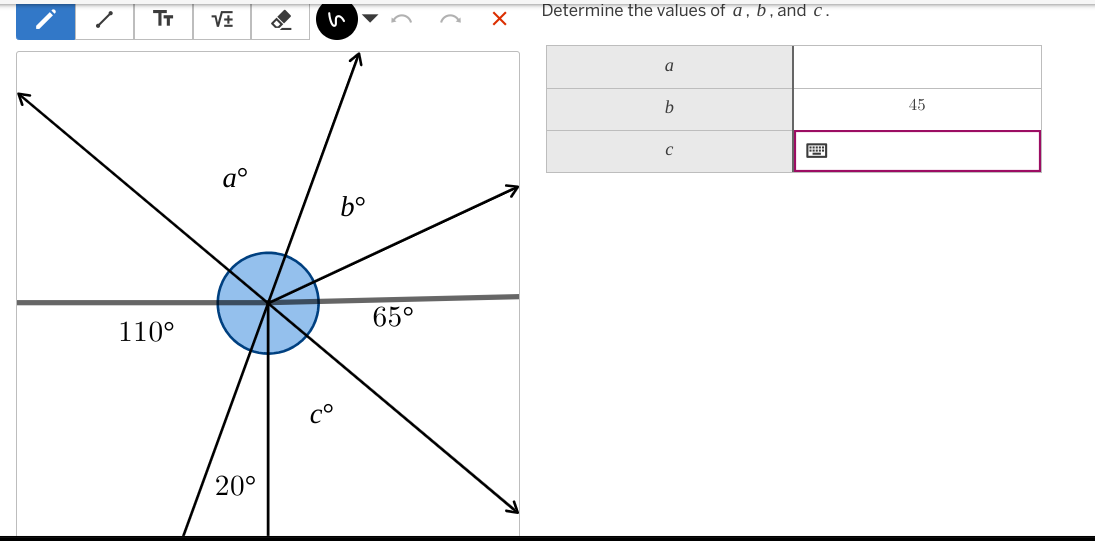
Determine the values of a, b, and c.
Understand the Problem
The question asks us to determine the values of angles a, b, and c given the information on the diagram. The key idea is to use properties of angles on a straight line, vertically opposite angles, and angles around a point to calculate the missing angle measurements.
Answer
$a = 90^\circ$ $b = 45^\circ$ $c = 20^\circ$
Answer for screen readers
$a = 90^\circ$ $b = 45^\circ$ $c = 20^\circ$
Steps to Solve
- Find the vertically opposite angle of $110^\circ$
Vertically opposite angles are equal. The angle opposite $110^\circ$ equals $a + 20^\circ$. Therefore: $a + 20^\circ = 110^\circ$
- Solve for $a$
Subtract $20^\circ$ from both sides of the equation: $a = 110^\circ - 20^\circ = 90^\circ$
- Find the vertically opposite angle of $65^\circ$
The angle opposite $65^\circ$ is $b + c$. Therefore: $b + c = 65^\circ$
- Substitute the given value of $b$ to find $c$
We are given that $b = 45^\circ$. Substitute this value into the equation $b + c = 65^\circ$: $45^\circ + c = 65^\circ$
- Solve for $c$
Subtract $45^\circ$ from both sides of the equation: $c = 65^\circ - 45^\circ = 20^\circ$
$a = 90^\circ$ $b = 45^\circ$ $c = 20^\circ$
More Information
Interesting geometric problems like this can be solved by recognizing relationships between angles such as vertically opposite angles and angles on a straight line.
Tips
A common mistake is not recognizing vertically opposite angles, or incorrectly setting up the equations. Careful examination of the diagram and verification of the solution can help avoid this.
AI-generated content may contain errors. Please verify critical information