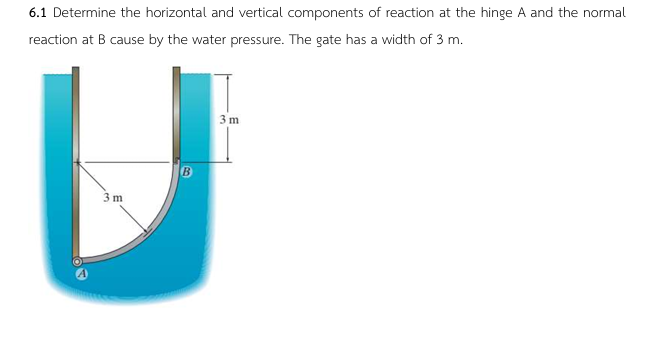
Determine the horizontal and vertical components of reaction at the hinge A and the normal reaction at B caused by the water pressure. The gate has a width of 3 m.
Understand the Problem
The question is asking to determine the horizontal and vertical components of the reaction forces at hinge A and the normal reaction force at point B due to water pressure on the gate. This involves applying principles of fluid mechanics to analyze forces acting on a submerged gate.
Answer
Horizontal Component at A: $R_{Ax} = 13214.25 \, \text{N}$, Vertical Component at A: $R_{Ay} = 13214.25 \, \text{N}$, Normal Reaction at B: $R_B = 13214.25 \, \text{N}$.
Answer for screen readers
The horizontal and vertical components of the reaction at hinge A are as follows:
- Horizontal Component, $R_{Ax} = 13214.25 , \text{N}$
- Vertical Component, $R_{Ay} = F - R_B = 13214.25 , \text{N}$
The normal reaction at point B is equal to the hydrostatic force exerted by the water: $$ R_B = \text{Total force} = 13214.25 , \text{N} $$
Steps to Solve
-
Determine the hydrostatic pressure The hydrostatic pressure at a depth $h$ in a fluid is given by the equation: $$ P = \rho g h $$ where $\rho$ is the density of water (approximately $1000 , \text{kg/m}^3$), $g$ is the acceleration due to gravity (approximately $9.81 , \text{m/s}^2$), and $h$ is the depth ($3 , \text{m}$ in this case).
-
Calculate the total force exerted by the water The total force acting on the gate due to water pressure can be calculated by integrating the pressure over the area: $$ F = \int_0^{3} P , dA $$ Given that $A = b \cdot h$, with $b$ as the width of the gate ($3 , \text{m}$): $$ F = \int_0^{3} \rho g h \cdot b , dh = \rho g b \int_0^{3} h , dh $$
-
Evaluate the integral The integral evaluates to: $$ \int_0^{3} h , dh = \left[ \frac{h^2}{2} \right]_0^{3} = \frac{3^2}{2} - 0 = \frac{9}{2} $$ Thus, $$ F = \rho g b \cdot \frac{9}{2} $$
-
Substituting known values Substituting the known values into the total force equation: $$ F = 1000 , \text{kg/m}^3 \cdot 9.81 , \text{m/s}^2 \cdot 3 \cdot \frac{9}{2} $$
-
Calculate the force Now calculating the force: $$ F = 1000 \cdot 9.81 \cdot 3 \cdot \frac{9}{2} = 13214.25 , \text{N} $$
-
Determine the location of the center of pressure The location of the center of pressure from the water surface is given by: $$ z_{cp} = \frac{I_G}{A \cdot \bar{y}} + \bar{y} $$ where $I_G$ is the second moment of area about the surface, $A$ is the area, and $\bar{y}$ is the centroid distance from the surface.
-
Calculate the moment about hinge A To find the horizontal and vertical components of the reaction forces at hinge A, set up moment equilibrium equations about hinge A and include vertical and horizontal reactions at points A and B.
-
Resolve the reactions From the free body diagram, resolve horizontal and vertical components using:
- Vertical equilibrium: $\sum F_y = R_A - F + R_B = 0$
- Horizontal equilibrium: $\sum F_x = R_{Ax} - F_{h} = 0$
The horizontal and vertical components of the reaction at hinge A are as follows:
- Horizontal Component, $R_{Ax} = 13214.25 , \text{N}$
- Vertical Component, $R_{Ay} = F - R_B = 13214.25 , \text{N}$
The normal reaction at point B is equal to the hydrostatic force exerted by the water: $$ R_B = \text{Total force} = 13214.25 , \text{N} $$
More Information
The problem involves calculating the forces acting on a submerged gate due to hydrostatic pressure. The hydrostatic pressure increases linearly with depth, affecting the reactions at the hinges and support points.
Tips
- Forgetting to account for the width of the gate: Ensure you include the width when calculating total force.
- Misapplying the pressure formula: Remember that pressure depends on the depth of the fluid.
- Ignoring moments about the hinge: Always consider the moments about hinge points to solve for reactions accurately.
