Determine the exact value of each expression. Simplify where possible. a) sin(π/3) * tan(π/6) / cos(π/4) b) tan(π/4) + tan(π/6) - tan(π/3)
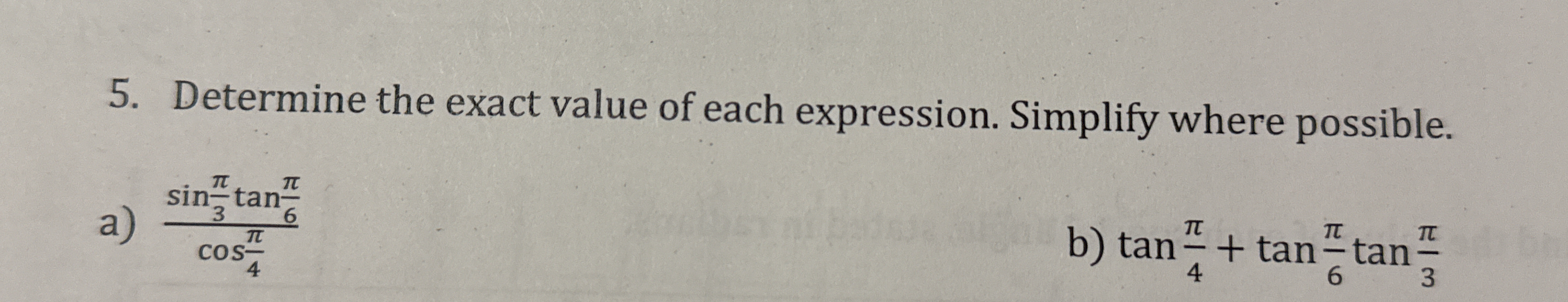
Understand the Problem
The question is asking to determine the exact values of trigonometric expressions and to simplify them where possible. This involves using known trigonometric identities and values for specific angles.
Answer
a) $\frac{\sqrt{2}}{2}$ b) $\frac{\sqrt{3} - 2}{\sqrt{3}}$
Answer for screen readers
a) The exact value of the expression is $\frac{\sqrt{2}}{2}$.
b) The exact value of the expression is $\frac{\sqrt{3} - 2}{\sqrt{3}}$.
Steps to Solve
-
Evaluate the trigonometric functions For part (a), we need to find the values of the following:
- $\sin(\frac{\pi}{3}) = \frac{\sqrt{3}}{2}$
- $\tan(\frac{\pi}{6}) = \frac{1}{\sqrt{3}}$
- $\cos(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}$
-
Substitute the values into the expression Now, substitute these values into the expression for part (a): $$ \frac{\sin(\frac{\pi}{3}) \cdot \tan(\frac{\pi}{6})}{\cos(\frac{\pi}{4})} = \frac{\left(\frac{\sqrt{3}}{2}\right) \cdot \left(\frac{1}{\sqrt{3}}\right)}{\frac{\sqrt{2}}{2}} $$
-
Simplify the expression Simplifying gives us: $$ \frac{\frac{\sqrt{3}}{2\sqrt{3}}}{\frac{\sqrt{2}}{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} $$
-
Evaluate the trigonometric functions for part (b) For part (b), find the values of the following:
- $\tan(\frac{\pi}{4}) = 1$
- $\tan(\frac{\pi}{6}) = \frac{1}{\sqrt{3}}$
- $\tan(\frac{\pi}{3}) = \sqrt{3}$
-
Substitute values into the expression for part (b) Substitute into the expression: $$ \tan(\frac{\pi}{4}) + \tan(\frac{\pi}{6}) - \tan(\frac{\pi}{3}) = 1 + \frac{1}{\sqrt{3}} - \sqrt{3} $$
-
Combine the terms To combine the terms into a single expression, we get: $$ 1 + \frac{1}{\sqrt{3}} - \sqrt{3} = 1 - \sqrt{3} + \frac{1}{\sqrt{3}} $$ To write it over a common denominator: $$ = \frac{\sqrt{3}}{\sqrt{3}} + \frac{1}{\sqrt{3}} - \frac{3}{\sqrt{3}} = \frac{\sqrt{3} + 1 - 3}{\sqrt{3}} = \frac{\sqrt{3} - 2}{\sqrt{3}} $$
a) The exact value of the expression is $\frac{\sqrt{2}}{2}$.
b) The exact value of the expression is $\frac{\sqrt{3} - 2}{\sqrt{3}}$.
More Information
- The sine, cosine, and tangent values for common angles can often be derived using the unit circle.
- The trigonometric identities and values are essential for simplifying these types of expressions.
Tips
- A common mistake is forgetting to simplify the expressions correctly after substitution.
- Another error is miscalculating the values of the trigonometric functions.
AI-generated content may contain errors. Please verify critical information