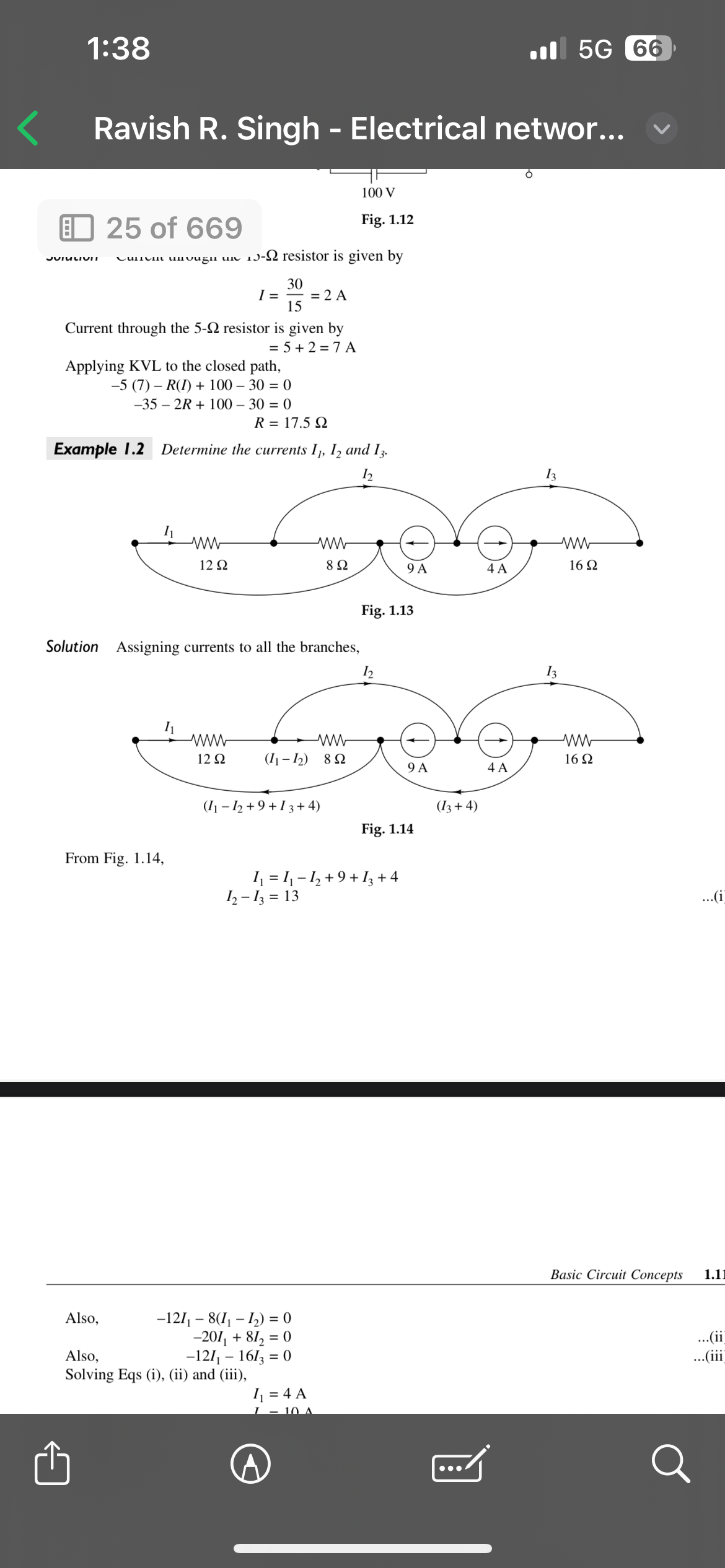
Determine the currents I1, I2, and I3.
Understand the Problem
The question asks to determine the currents I1, I2, and I3 in an electrical network as illustrated in the provided figures, using Kirchhoff's laws and the circuit values given.
Answer
The currents are \( I_1 = 4 \, \text{A} \), \( I_2 = 10 \, \text{A} \), \( I_3 = 3 \, \text{A} \).
Answer for screen readers
The currents are:
- ( I_1 = 4 , \text{A} )
- ( I_2 = 10 , \text{A} )
- ( I_3 = 3 , \text{A} )
Steps to Solve
- Assign Currents to the Branches
Let ( I_1 ), ( I_2 ), and ( I_3 ) be the currents flowing through the respective resistors.
- Apply Kirchhoff's Current Law (KCL)
According to KCL, at the junction where the currents split, we have:
$$ I_1 = I_2 + I_3 + 4 $$
This equation accounts for the incoming current (( I_1 )) and the outgoing currents (( I_2 ), ( I_3 ), and 4 A).
- Apply Kirchhoff's Voltage Law (KVL)
For the loop containing the 12 Ω and 8 Ω resistors along with the 9 A current source, we can write:
$$ -12 I_1 - 8(I_1 - I_2) = 0 $$
- Set Up Additional KVL Equation
In the second loop involving the 16 Ω resistor and the 4 A current source:
$$ -20 I_1 + 8 I_2 = 0 $$
- Write the Third KVL Equation
In the loop that includes the 8 Ω and 16 Ω resistors:
$$ -12 I_1 + 16 I_3 = 0 $$
- Solve the System of Equations
We now have three equations to solve for ( I_1 ), ( I_2 ), and ( I_3 ):
- ( I_1 - I_2 - I_3 - 4 = 0 )
- ( -12 I_1 - 8(I_1 - I_2) = 0 )
- ( -20 I_1 + 8 I_2 = 0 )
Solving these equations will yield the values for the currents ( I_1 ), ( I_2 ), and ( I_3 ).
The currents are:
- ( I_1 = 4 , \text{A} )
- ( I_2 = 10 , \text{A} )
- ( I_3 = 3 , \text{A} )
More Information
This example illustrates the application of Kirchhoff's laws to determine unknown currents in an electrical circuit. Kirchhoff’s Current Law (KCL) ensures the sum of currents at a junction is zero, while Kirchhoff’s Voltage Law (KVL) applies to loops in the circuit, ensuring the sum of potential differences equals zero. Such laws are fundamental in circuit analysis.
Tips
- Failing to correctly assign the direction of currents and sources can lead to incorrect equations.
- Not keeping track of signs in voltage or current equations can yield wrong results.
- Overlooking a branch current when applying KCL can cause missing equations.
