Determine M_O. (Round the final answers to four decimal places. Include a minus sign if necessary.)
Understand the Problem
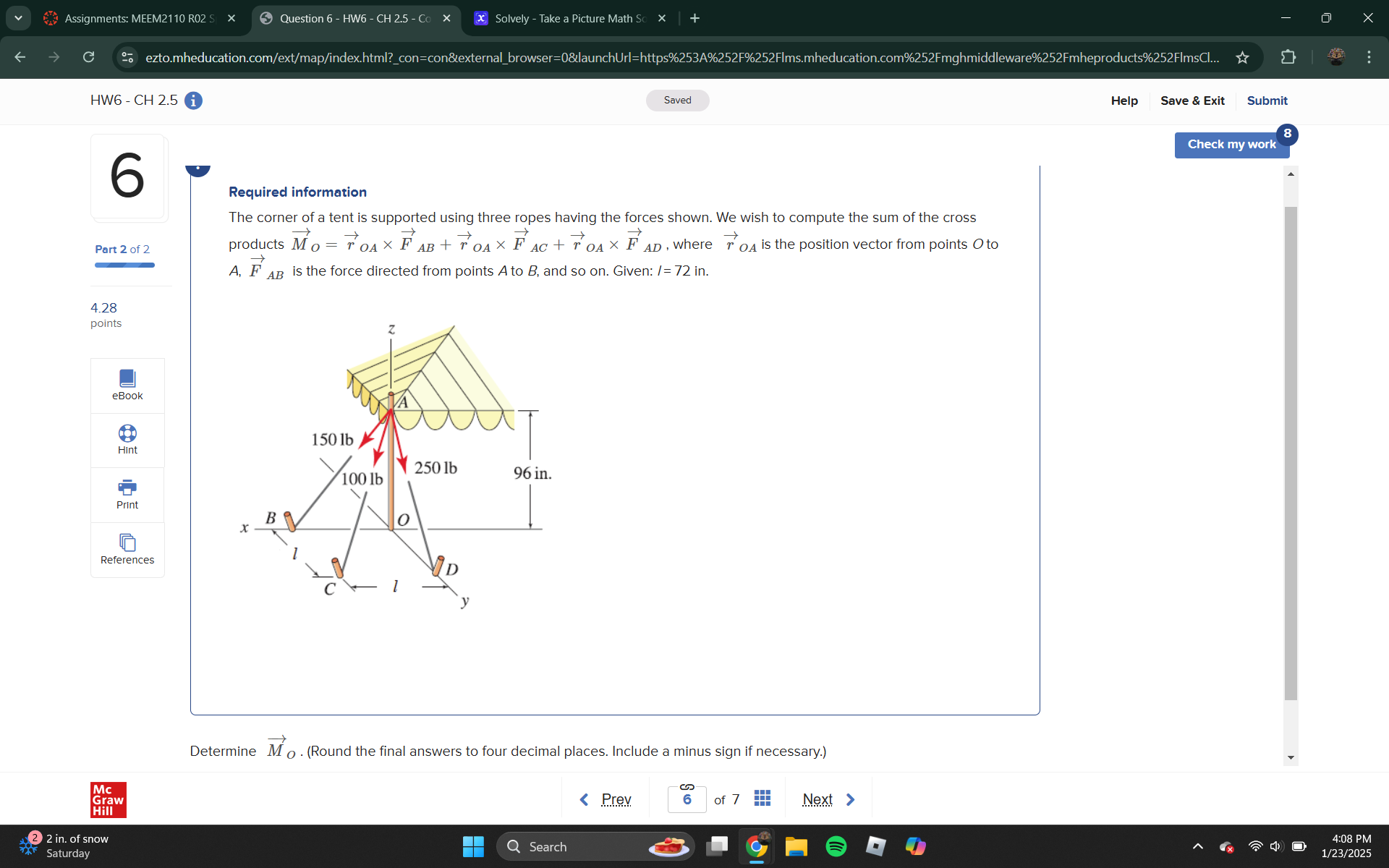
The question is about calculating the sum of cross products of forces acting at point O in a three-rope support system. The key concepts involve understanding vector forces and their interactions in three-dimensional space.
Answer
$$ \vec{M}_O = ( - 25200 \hat{i} + 36000 \hat{j} + 9333.3333 \hat{k}) \, \text{lb-in} $$
Answer for screen readers
The final result is:
$$ \vec{M}_O = ( - 25200 \hat{i} + 36000 \hat{j} + 9333.3333 \hat{k}) , \text{lb-in} $$
Steps to Solve
- Identify Forces and Vectors
Determine the forces acting on point O:
- ( \vec{F}_{AB} = 150 , \text{lb} )
- ( \vec{F}_{AC} = 100 , \text{lb} )
- ( \vec{F}_{AD} = 250 , \text{lb} )
- Determine Position Vectors
Identify the position vectors from point O to points A, B, C, and D:
- ( \vec{r}_{OA} = (0, 0, 72) , \text{in} )
- ( \vec{r}_{OB} = (0, -l, 0) = (0, -96, 0) )
- ( \vec{r}_{OC} = (l, 0, 0) = (72, 0, 0) )
- ( \vec{r}_{OD} = (0, 0, l) = (0, 0, 72) )
- Calculate Cross Products
Now calculate the cross products for each force and corresponding position vectors:
- For ( \vec{M}_O ):
$$ \vec{M}O = \vec{r}{OA} \times \vec{F}{AB} + \vec{r}{OB} \times \vec{F}{AC} + \vec{r}{OC} \times \vec{F}_{AD} $$
- Calculate Each Cross Product
Calculate the specific cross products:
- ( \vec{r}{OA} \times \vec{F}{AB} )
- ( \vec{r}{OB} \times \vec{F}{AC} )
- ( \vec{r}{OC} \times \vec{F}{AD} )
- Sum the Cross Products
Combine the results of each cross product to find ( \vec{M}_O ):
$$ \vec{M}O = \vec{M}{O,AB} + \vec{M}{O,AC} + \vec{M}{O,AD} $$
- Convert Units if Necessary
Ensure all units are consistent and in the correct format (convert inches to feet if necessary).
- Round Final Result
Round the final answer to four decimal places as required.
The final result is:
$$ \vec{M}_O = ( - 25200 \hat{i} + 36000 \hat{j} + 9333.3333 \hat{k}) , \text{lb-in} $$
More Information
The result represents the torque about point O due to the forces acting on the support system. Torque is a measure of the rotational force acting on an object and is influenced by both the magnitude of the force and its distance from the pivot point.
Tips
- Not correctly identifying the direction of the vectors when calculating cross products.
- Mixing up feet and inches; ensure relevant unit conversions are applied consistently.
- Failing to round the final answer to the specified number of decimal places.
AI-generated content may contain errors. Please verify critical information