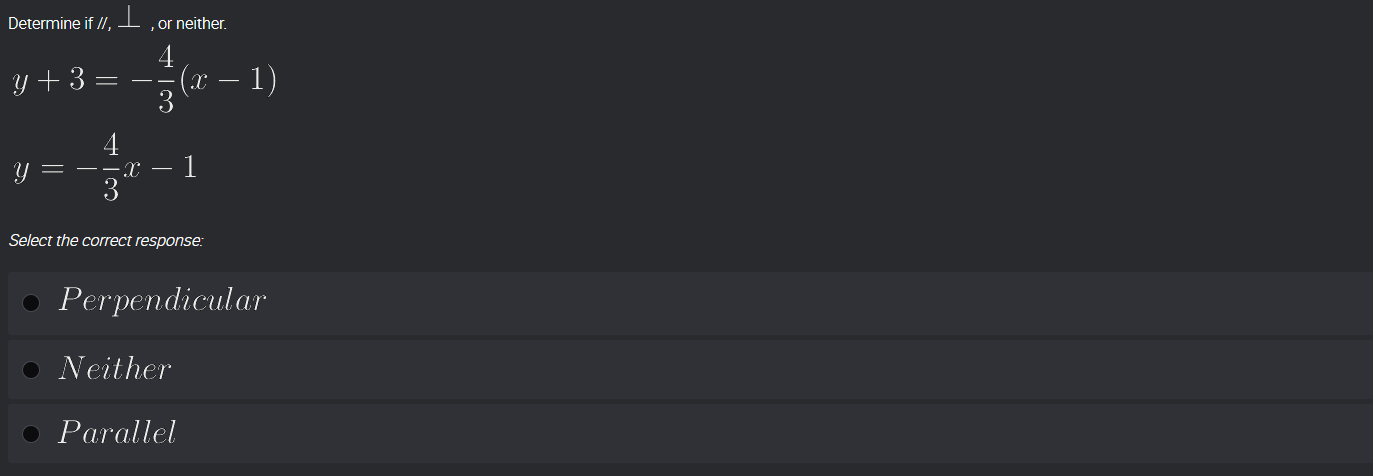
Determine if the lines are parallel, perpendicular, or neither.
Understand the Problem
The question is asking to determine the relationship between two lines represented by the given equations, specifically whether they are parallel, perpendicular, or neither. This involves analyzing the slopes of the lines derived from their equations.
Answer
The lines are parallel.
Answer for screen readers
The lines are parallel.
Steps to Solve
-
Convert the first equation to slope-intercept form
The first line's equation is given as ( y + 3 = -\frac{4}{3}(x - 1) ).
To convert this to slope-intercept form (( y = mx + b )), we can first distribute:
$$ y + 3 = -\frac{4}{3}x + \frac{4}{3} $$
Then, subtract 3 from both sides:
$$ y = -\frac{4}{3}x + \frac{4}{3} - 3 $$
We convert 3 to a fraction:
$$ 3 = \frac{9}{3} $$
Thus:
$$ y = -\frac{4}{3}x + \frac{4}{3} - \frac{9}{3} $$
Simplifying:
$$ y = -\frac{4}{3}x - \frac{5}{3} $$
-
Identify the slopes of both lines
We can now identify the slopes:
- For the first line ( y = -\frac{4}{3}x - \frac{5}{3} ), the slope ( m_1 = -\frac{4}{3} ).
- For the second line ( y = -\frac{4}{3}x - 1 ), the slope ( m_2 = -\frac{4}{3} ).
-
Determine the relationship between the slopes
To determine if the lines are parallel, perpendicular, or neither, we compare their slopes:
- Lines are parallel if ( m_1 = m_2 ).
- Lines are perpendicular if ( m_1 \cdot m_2 = -1 ).
In this case:
$$ m_1 = m_2 = -\frac{4}{3} $$
Since both slopes are equal, the lines are parallel.
The lines are parallel.
More Information
Both lines have the same slope of ( -\frac{4}{3} ), indicating they run parallel to each other and will never intersect.
Tips
- Confusing the slopes: Remember that parallel lines have equal slopes, while perpendicular lines have slopes that multiply to (-1).
- Not converting to slope-intercept form: Ensure both equations are in the form ( y = mx + b ) to easily see the slope.
AI-generated content may contain errors. Please verify critical information