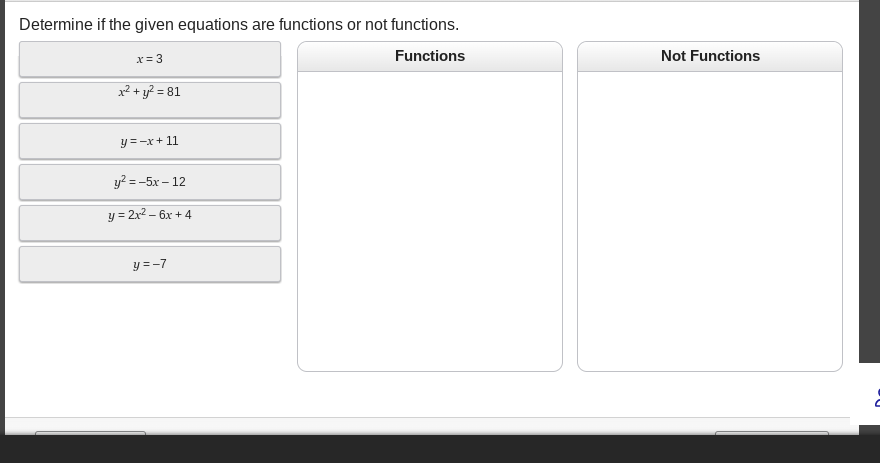
Determine if the given equations are functions or not functions.
Understand the Problem
The question is asking to determine if given equations are functions or not functions. This requires analyzing each equation to see if it meets the criteria for being a function, which can be tested by the vertical line test or examining if each input corresponds to exactly one output.
Answer
Functions: $y = -x + 11$, $y = 2x^2 - 6x + 4$, $y = -7$; Not Functions: $x = 3$, $x^2 + y^2 = 81$, $y^2 = -5x - 12$.
Answer for screen readers
Functions:
- $y = -x + 11$
- $y = 2x^2 - 6x + 4$
- $y = -7$
Not Functions:
- $x = 3$
- $x^2 + y^2 = 81$
- $y^2 = -5x - 12$
Steps to Solve
-
Identify each equation For each equation, determine if it can produce only one output for each input.
-
Analyze the equations
-
The first equation is $x = 3$. This is a vertical line, which does not pass the vertical line test; therefore, it is not a function.
-
The second equation is $x^2 + y^2 = 81$. This represents a circle. For some $x$ values, there will be two corresponding $y$ values, so it is not a function.
-
The third equation is $y = -x + 11$. This is a linear equation, and for each $x$, there is exactly one $y$. Thus, it is a function.
-
The fourth equation is $y^2 = -5x - 12$. This can lead to two $y$ values for some $x$ values, so it is not a function.
-
The fifth equation is $y = 2x^2 - 6x + 4$. This is a quadratic equation, which is a parabola. For each $x$, there is exactly one $y$, so it is a function.
-
The sixth equation is $y = -7$. This gives a constant output (a horizontal line), thus it is a function.
- Classify each equation Based on the analysis:
- Functions: $y = -x + 11$, $y = 2x^2 - 6x + 4$, $y = -7$.
- Not Functions: $x = 3$, $x^2 + y^2 = 81$, $y^2 = -5x - 12$.
Functions:
- $y = -x + 11$
- $y = 2x^2 - 6x + 4$
- $y = -7$
Not Functions:
- $x = 3$
- $x^2 + y^2 = 81$
- $y^2 = -5x - 12$
More Information
Understanding whether an equation is a function helps clarify how variables relate to one another. Functions have unique outputs for each input, which is essential for modeling many real-world scenarios.
Tips
- Confusing linear equations with other types; always check if an equation can produce multiple outputs.
- Misunderstanding geometric shapes; equations like circles lead to multiple outputs for some inputs.
AI-generated content may contain errors. Please verify critical information