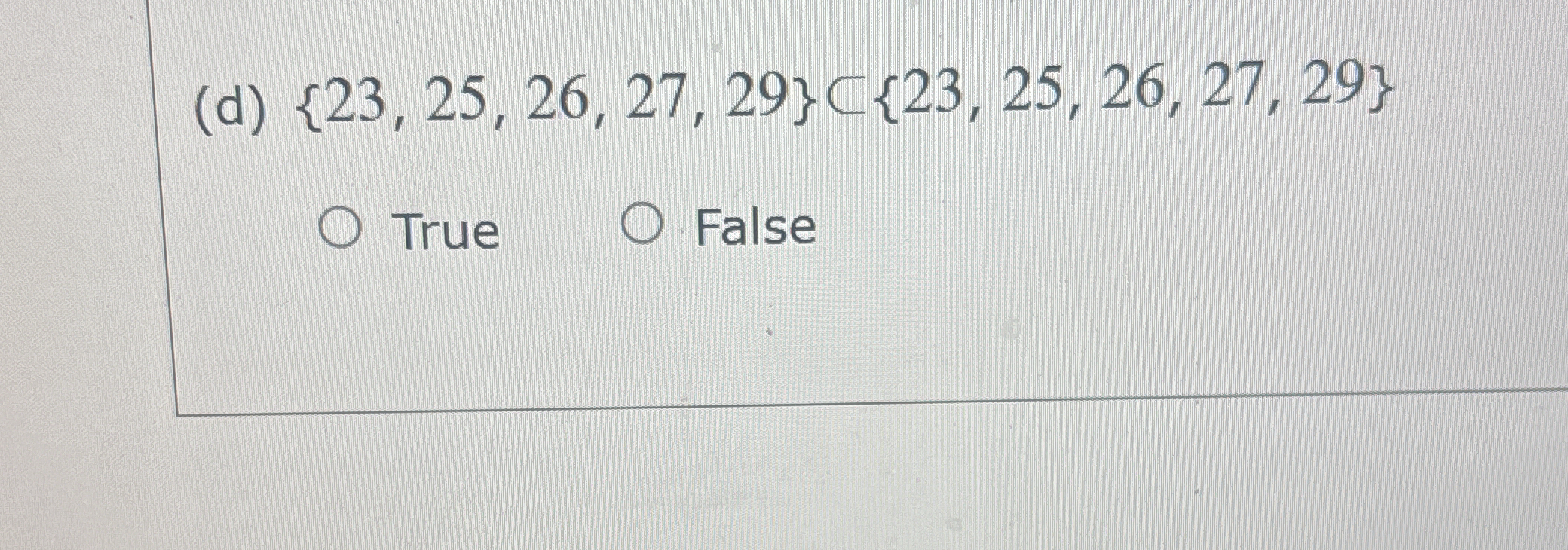
Determine if {23, 25, 26, 27, 29} is a proper subset of {23, 25, 26, 27, 29}.

Steps to Solve

1. Understand the definition of a proper subset A proper subset is a subset that is not equal to the original set. Set $A$ is a proper subset of set $B$ if all elements of $A$ are in $B$, and $A$ is not equal to $B$.

2. Compare the two sets We are given the set {23, 25, 26, 27, 29} and we are asked if it is a proper subset of {23, 25, 26, 27, 29}.

3. Check if all elements of the first set are in the second set All of the elements in the first set are present in the second set.

4. Check if the two sets are equal The two sets are equal since they contain exactly the same elements.

5. Determine if the first set is a proper subset of the second set Since the two sets are equal, the first set is not a proper subset of the second set. A proper subset must be strictly smaller than the original set.