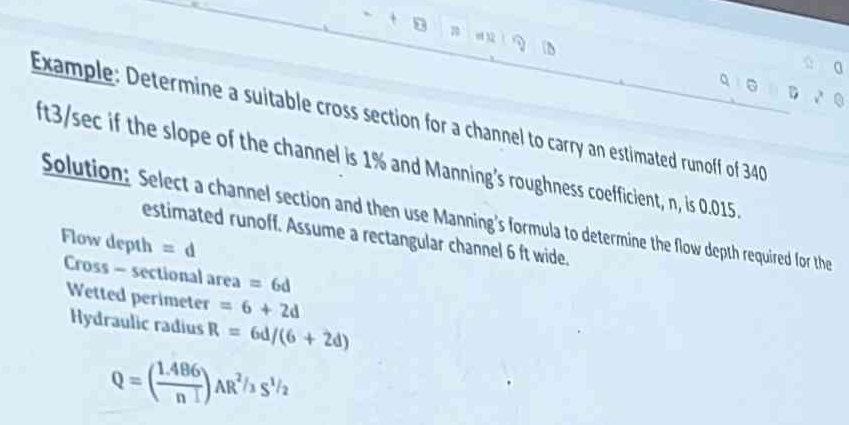
Determine a suitable cross section for a channel to carry an estimated runoff of 340 ft³/sec if the slope of the channel is 1% and Manning's roughness coefficient, n, is 0.015. Ass... Determine a suitable cross section for a channel to carry an estimated runoff of 340 ft³/sec if the slope of the channel is 1% and Manning's roughness coefficient, n, is 0.015. Assume a rectangular channel 6 ft wide. Read more

Steps to Solve

1. Define the variables

$Q = 340 , \text{ft}^3/\text{sec}$ (flow rate) $n = 0.015$ (Manning's roughness coefficient) $S = 0.01$ (channel slope) $b = 6 , \text{ft}$ (channel width) $d$ = flow depth (what we want to find)

2. Write the formulas

$A = bd = 6d$ (cross-sectional area) $P = b + 2d = 6 + 2d$ (wetted perimeter) $R = \frac{A}{P} = \frac{6d}{6 + 2d}$ (hydraulic radius) $Q = \frac{1.486}{n}AR^{2/3}S^{1/2}$ (Manning's formula)

3. Substitute the known values into Manning's formula

$$ 340 = \frac{1.486}{0.015} (6d)\left(\frac{6d}{6 + 2d}\right)^{2/3}(0.01)^{1/2} $$

4. Simplify the equation

$$ 340 = \frac{1.486}{0.015} (6d)\left(\frac{6d}{6 + 2d}\right)^{2/3}(0.1) $$

$$ 340 = \frac{1.486}{0.015} \cdot 6 \cdot 0.1 \cdot d \cdot \left(\frac{6d}{6 + 2d}\right)^{2/3} $$

$$ 340 = 59.44 \cdot d \cdot \left(\frac{6d}{6 + 2d}\right)^{2/3} $$

5. Solve for $d$ $$ \frac{340}{59.44} = d \cdot \left(\frac{6d}{6 + 2d}\right)^{2/3} $$

$$ 5.72 = d \cdot \left(\frac{6d}{6 + 2d}\right)^{2/3} $$ Solving for $d$ analytically is difficult, so we can use numerical methods or approximations. By trial and error, or using a numerical solver, we find that $d \approx 2.7 , \text{ft}$.