Degree of the differential equation sin x + cos(dy/dx) = y^2
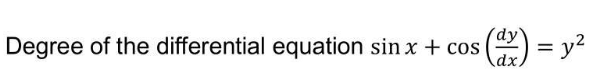
Understand the Problem
The question is asking for the degree of a given differential equation. The degree of a differential equation is determined by identifying the highest power of the highest derivative present when the equation is expressed in a polynomial form.
Answer
The degree is not defined.
Answer for screen readers
The degree of the differential equation is not defined.
Steps to Solve
-
Identify the highest derivative Look at the equation ( \sin x + \cos\left(\frac{dy}{dx}\right) = y^2 ). The highest derivative present is ( \frac{dy}{dx} ).
-
Rearrange to polynomial form To determine the degree, we need to express the equation in a form that isolates derivatives. Here, we express it as: $$ \cos\left(\frac{dy}{dx}\right) = y^2 - \sin x $$
-
Examine the structure of the equation In the polynomial form, the term ( \cos\left(\frac{dy}{dx}\right) ) is non-polynomial due to the cosine function. We cannot express it as a polynomial function of ( \frac{dy}{dx} ).
-
Conclude the degree Since the equation cannot be restructured into a polynomial form without transcendental functions, we conclude that the degree of the differential equation is not defined.
The degree of the differential equation is not defined.
More Information
Determining the degree of a differential equation requires it to be in polynomial form in terms of derivatives. However, if transcendental functions (like sine or cosine) are involved, the degree cannot be assessed.
Tips
null
