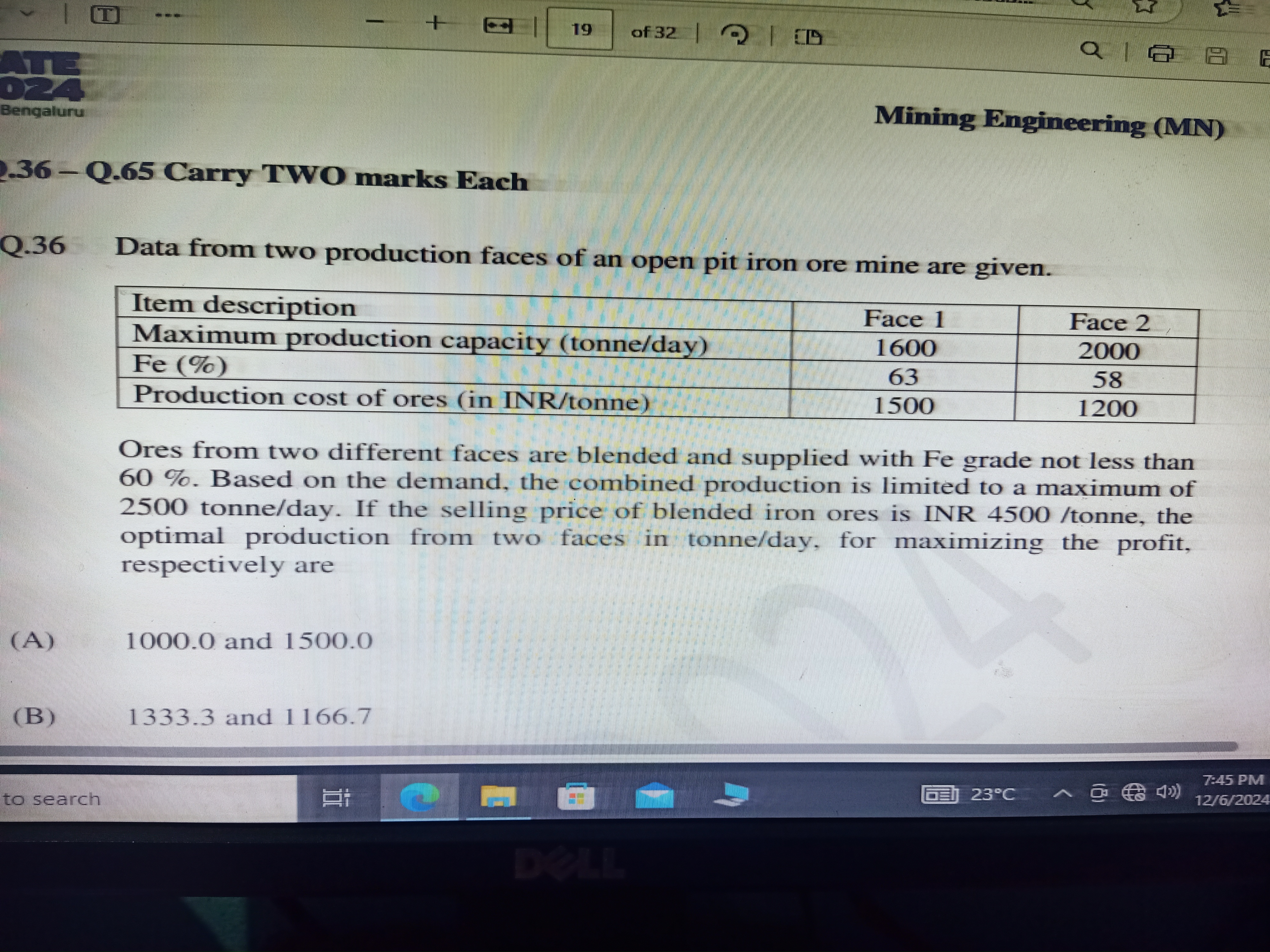
Data from two production faces of an open pit iron ore mine are given. Ores from two different faces are blended and supplied with Fe grade not less than 60%. Based on the demand,... Data from two production faces of an open pit iron ore mine are given. Ores from two different faces are blended and supplied with Fe grade not less than 60%. Based on the demand, the combined production is limited to a maximum of 2500 tonne/day. If the selling price of blended iron ores is INR 4500/tonne, the optimal production from two faces in tonne/day, for maximizing the profit, respectively are?
Understand the Problem
The question is asking about optimizing production from two different faces of an open pit iron ore mine while adhering to specific constraints on production capacity and quality of iron. The objective is to find the optimal production amounts from each face to maximize profit under given conditions.
Answer
The optimal production amounts are \( x_1 = 1000 \) tonnes and \( x_2 = 1500 \) tonnes.
Answer for screen readers
The optimal production amounts are ( x_1 = 1000 ) tonnes from Face 1 and ( x_2 = 1500 ) tonnes from Face 2.
Steps to Solve
-
Define the Variables Let ( x_1 ) be the amount of ore produced from Face 1 (in tonnes), and ( x_2 ) be the amount of ore produced from Face 2 (in tonnes).
-
Set Up the Objective Function Our goal is to maximize profit. The profit from Face 1 is ( (4500 - 1500)x_1 ) and from Face 2 is ( (4500 - 1200)x_2 ). Thus, the objective function is: $$ P = (4500 - 1500)x_1 + (4500 - 1200)x_2 = 3000x_1 + 3300x_2 $$
-
List the Constraints We have the following constraints:
- ( x_1 + x_2 \leq 2500 ) (production limit)
- ( x_1 \leq 1600 ) (Face 1 capacity)
- ( x_2 \leq 2000 ) (Face 2 capacity)
- ( 0 \leq x_1, x_2 ) (non-negativity)
-
Formulate the Linear Programming Problem Maximize: $$ P = 3000x_1 + 3300x_2 $$ Subject to: $$ \begin{aligned} x_1 + x_2 & \leq 2500\ x_1 & \leq 1600\ x_2 & \leq 2000\ x_1, x_2 & \geq 0 \end{aligned} $$
-
Graph the Constraints Graphically plot the constraints to find the feasible region.
-
Find the Corner Points Identify the corner points of the feasible region, which are potential candidates for maximization.
-
Calculate the Profit at Each Corner Point Evaluate the objective function ( P ) at each corner point.
-
Identify the Optimal Solution Select the corner point that yields the highest profit.
The optimal production amounts are ( x_1 = 1000 ) tonnes from Face 1 and ( x_2 = 1500 ) tonnes from Face 2.
More Information
The profit maximized comes from balancing production while adhering to constraints. This problem is an application of linear programming, commonly used in various fields for optimizing resource allocation.
Tips
- Confusing the constraints when summing ( x_1 ) and ( x_2 ). Remember to respect the maximum capacities strictly.
- Neglecting non-negativity constraints, leading to impossible production scenarios.
AI-generated content may contain errors. Please verify critical information