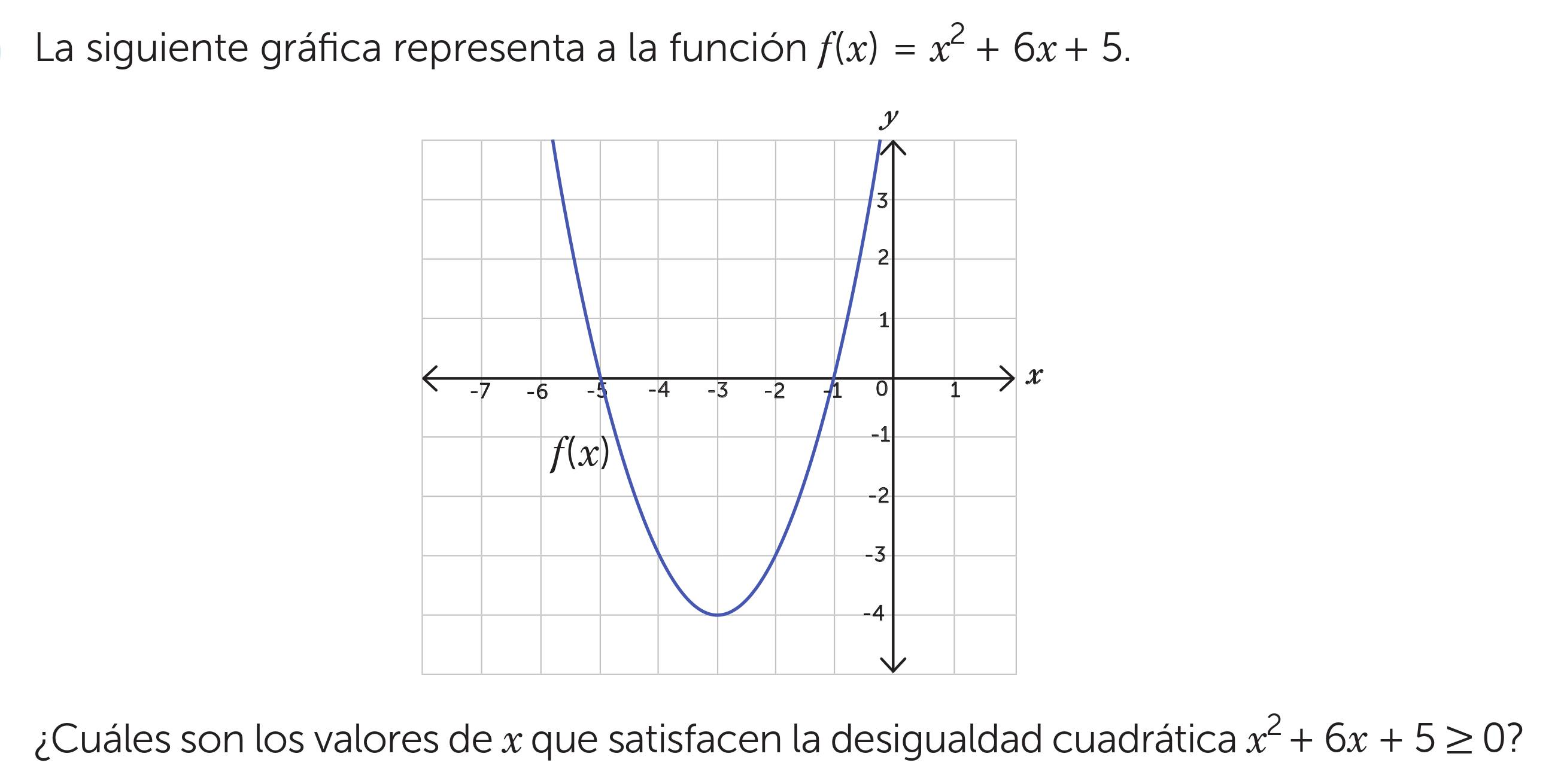
Dada la gráfica de la función f(x) = x² + 6x + 5, ¿cuáles son los valores de x que satisfacen la desigualdad cuadrática x² + 6x + 5 ≥ 0?
Understand the Problem
La pregunta presenta una gráfica de la función cuadrática f(x) = x² + 6x + 5 y pide encontrar los valores de x que satisfacen la desigualdad x² + 6x + 5 ≥ 0. Esto significa determinar para qué valores de x la función es mayor o igual a cero, lo cual se puede identificar observando dónde la gráfica está por encima o sobre el eje x.
Answer
$(-\infty, -5] \cup [-1, \infty)$
Answer for screen readers
$(-\infty, -5] \cup [-1, \infty)$
Steps to Solve
- Identify the x-intercepts
The $x$-intercepts are the points where the graph intersects the $x$-axis (i.e., where $f(x) = 0$). From the graph, we can see that the $x$-intercepts are at $x = -5$ and $x = -1$.
- Determine where the function is greater than or equal to zero
The inequality $x^2 + 6x + 5 \geq 0$ is satisfied when the graph of the function $f(x) = x^2 + 6x + 5$ is above or on the $x$-axis.
- Express the solution as an interval
The graph is above or on the $x$-axis for $x \leq -5$ and $x \geq -1$. In interval notation, this is $(-\infty, -5] \cup [-1, \infty)$.
$(-\infty, -5] \cup [-1, \infty)$
More Information
The solution to the inequality $x^2 + 6x + 5 \geq 0$ represents the set of all $x$ values for which the quadratic function $f(x) = x^2 + 6x + 5$ is non-negative. This corresponds to regions where the parabola is above or touching the x-axis.
Tips
A common mistake is to only consider the region between the roots, i.e., $-5 \le x \le -1$, where the function is less than or equal to zero. Also, one might forget to include the roots themselves, where $f(x) = 0$, since the inequality is greater than or equal to zero.
AI-generated content may contain errors. Please verify critical information