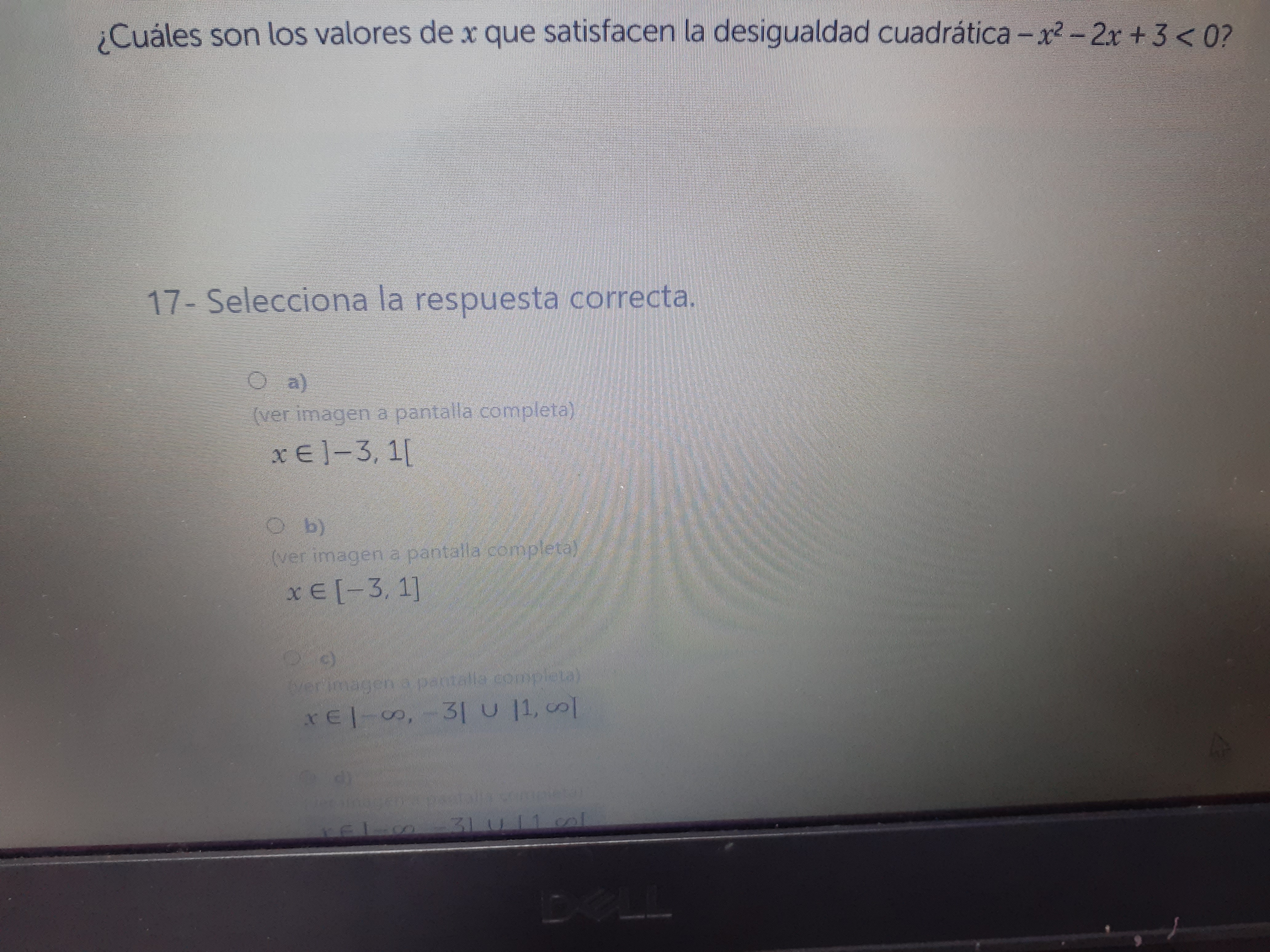
¿Cuáles son los valores de x que satisfacen la desigualdad cuadrática -x² - 2x + 3 < 0?

Steps to Solve

1. Multiply by -1 to simplify To make the quadratic easier to work with, multiply both sides of the inequality by -1. Remember to flip the inequality sign: $$-x^2 - 2x + 3 < 0$$ $$x^2 + 2x - 3 > 0$$

2. Factor the quadratic expression Factor the quadratic expression $x^2 + 2x - 3$: $$(x+3)(x-1) > 0$$

3. Find the critical points The critical points are the values of $x$ that make the expression equal to zero: $$x+3 = 0 \Rightarrow x = -3$$ $$x-1 = 0 \Rightarrow x = 1$$

4. Test intervals The critical points divide the number line into three intervals: $(-\infty, -3)$, $(-3, 1)$, and $(1, \infty)$. We need to test a value from each interval in the inequality $(x+3)(x-1) > 0$ to see if it satisfies the inequality.

• Interval $(-\infty, -3)$: Choose $x = -4$. Then $(-4+3)(-4-1) = (-1)(-5) = 5 > 0$. So, this interval is part of the solution

• Interval $(-3, 1)$: Choose $x = 0$. Then $(0+3)(0-1) = (3)(-1) = -3 < 0$. So, this interval is not part of the solution.

• Interval $(1, \infty)$: Choose $x = 2$. Then $(2+3)(2-1) = (5)(1) = 5 > 0$. So, this interval is part of the solution.

5. Write the solution in interval notation Since we are looking for where the expression is strictly greater than 0, we use parentheses (not brackets) to denote the intervals. The solution is the union of the intervals $(-\infty, -3)$ and $(1, \infty)$. $$x \in (-\infty, -3) \cup (1, \infty)$$