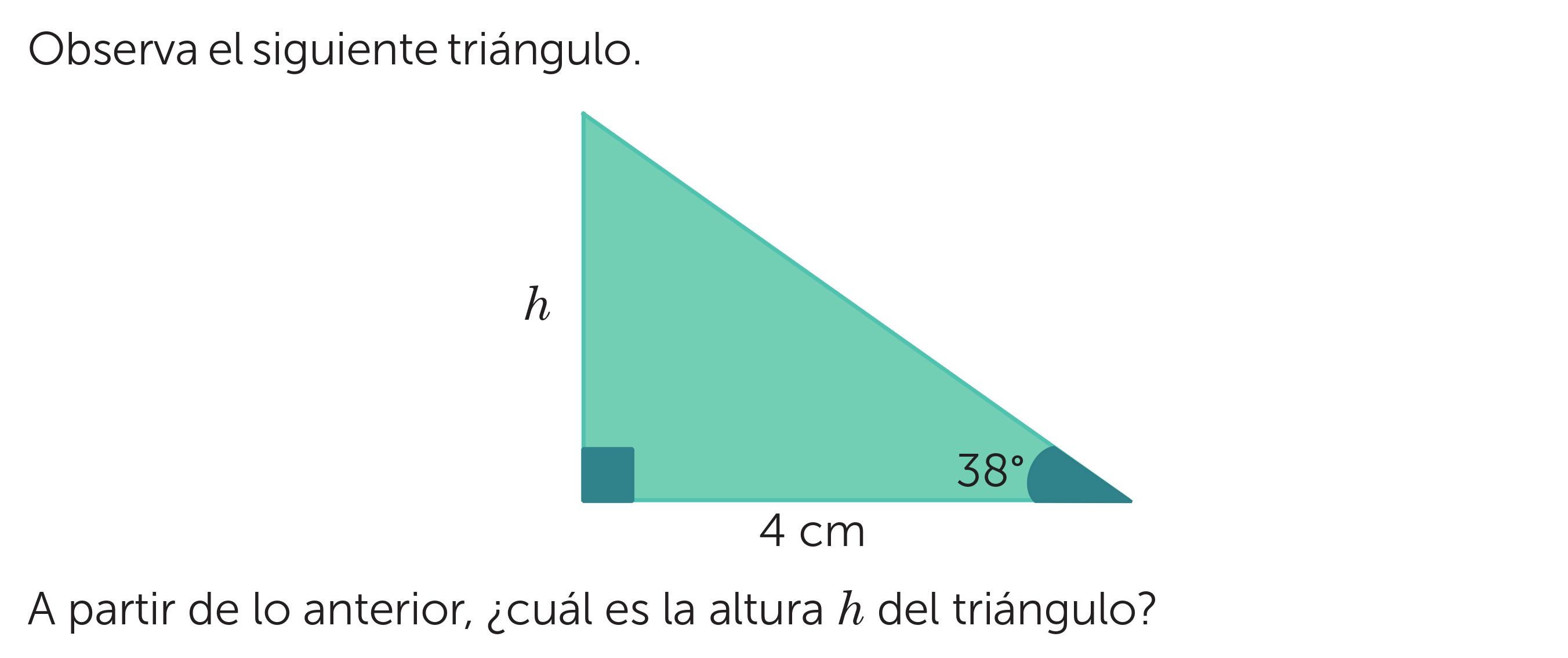
¿Cuál es la altura h del triángulo a partir de la siguiente información: un ángulo de 38 grados y la longitud del lado adyacente a ese ángulo, que es de 4 cm?

Understand the Problem

La pregunta pide calcular la altura h de un triángulo rectángulo, dado un ángulo de 38 grados y la longitud del lado adyacente a ese ángulo, que es de 4 cm. Se puede resolver usando la función trigonométrica tangente.

Answer

$h \approx 3.13 \text{ cm}$

Steps to Solve

Identificar la relación trigonométrica

Como tenemos el ángulo y la longitud del lado adyacente, y queremos encontrar la longitud del lado opuesto (altura $h$), podemos usar la función tangente: $$ \tan(\theta) = \frac{\text{lado opuesto}}{\text{lado adyacente}} $$

Sustituir los valores conocidos

Sustituimos $\theta = 38^\circ$ y lado adyacente $= 4$ cm en la ecuación: $$ \tan(38^\circ) = \frac{h}{4} $$

Resolver para $h$

Multiplicamos ambos lados de la ecuación por 4 para despejar $h$: $$ h = 4 \cdot \tan(38^\circ) $$

Calcular el valor de $h$

Usamos una calculadora para encontrar el valor de $\tan(38^\circ)$ y luego multiplicamos por 4: $$ h = 4 \cdot 0.7813 \approx 3.1252 $$ Por lo tanto, $h \approx 3.13$ cm.

$h \approx 3.13 \text{ cm}$

More Information

La tangente del ángulo es la razón entre el lado opuesto y el lado adyacente. En un triángulo rectángulo, esta relación es fundamental para encontrar lados desconocidos cuando se conocen ángulos y otros lados.

Tips

Usar la función seno o coseno en lugar de la tangente. La elección de la función trigonométrica correcta es crucial; seno se usa para la relación entre el lado opuesto y la hipotenusa, coseno para la relación entre el lado adyacente y la hipotenusa, y tangente para la relación entre el lado opuesto y el lado adyacente.
No asegurarse de que la calculadora esté en modo de grados (degrees) al calcular la tangente de 38 grados. Si la calculadora está en radianes, el resultado será incorrecto.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!