∫ cot(θ) dθ
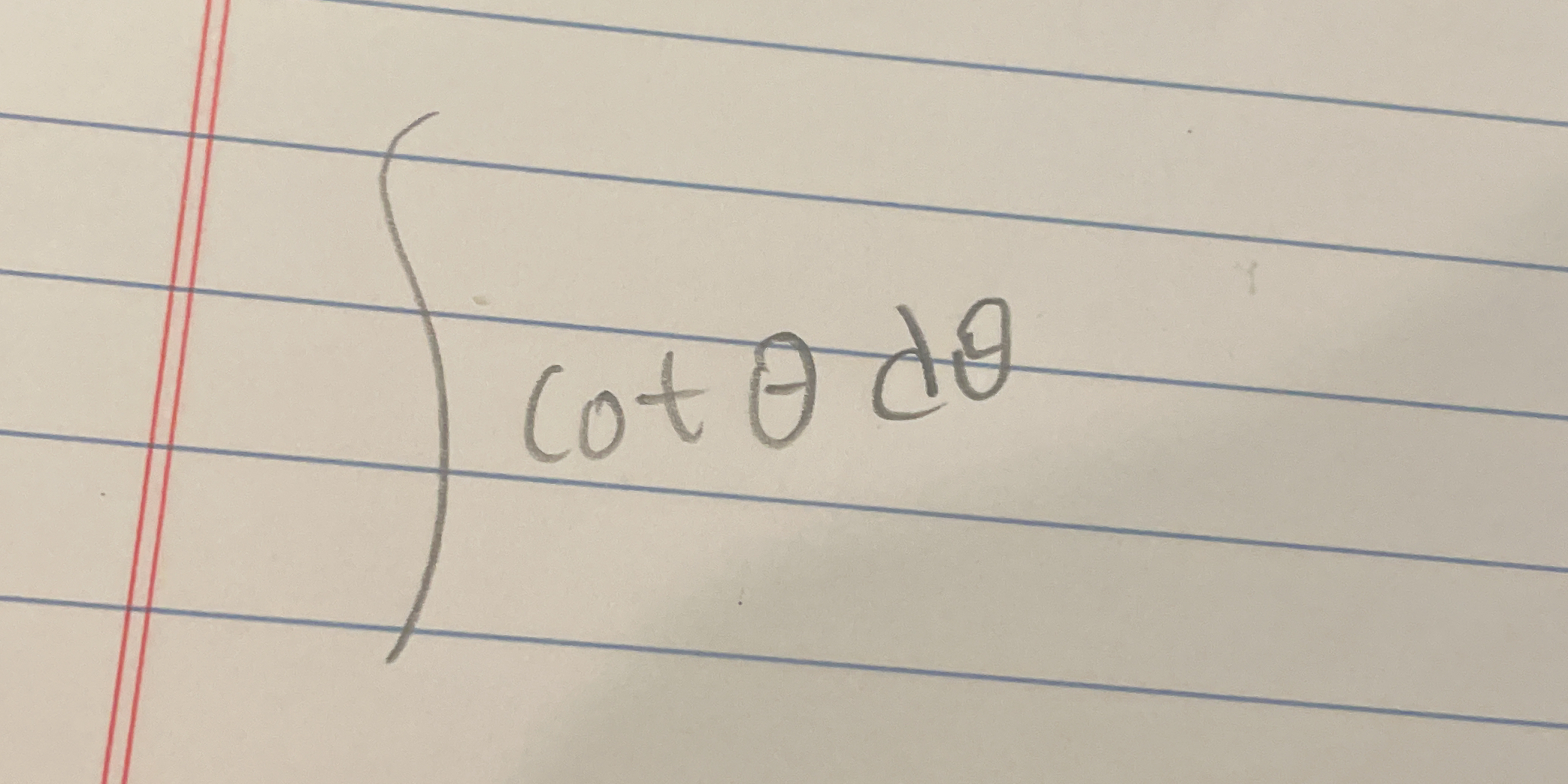
Understand the Problem
The question involves integrating the function cot(θ) with respect to θ. This is a trigonometric integral that requires knowledge of integration techniques specific to trigonometric functions.
Answer
$$ \int \cot(\theta) d\theta = \ln|\sin(\theta)| + C $$
Answer for screen readers
The final answer is: $$ \int \cot(\theta) d\theta = \ln|\sin(\theta)| + C $$
Steps to Solve
- Rewrite cotangent in terms of sine and cosine
The cotangent function can be rewritten as: $$ \cot(\theta) = \frac{\cos(\theta)}{\sin(\theta)} $$
- Use substitution
Let ( u = \sin(\theta) ). Then, the differential ( du ) is given by: $$ du = \cos(\theta) d\theta $$
Now, we can replace ( d\theta ): $$ d\theta = \frac{du}{\cos(\theta)} $$
This converts our integral: $$ \int \cot(\theta) d\theta = \int \frac{\cos(\theta)}{u} \cdot \frac{du}{\cos(\theta)} = \int \frac{1}{u} du $$
- Integrate
The integral of (\frac{1}{u}) is: $$ \int \frac{1}{u} du = \ln|u| + C $$
- Substitute back
Now substitute back ( u ): $$ \ln|u| + C = \ln|\sin(\theta)| + C $$
The final answer is: $$ \int \cot(\theta) d\theta = \ln|\sin(\theta)| + C $$
More Information
The integration of ( \cot(\theta) ) leads to the logarithm of the sine function, which highlights the relationship between trigonometric functions and logarithmic expressions. This integral is commonly encountered in calculus, especially in trigonometric integration.
Tips
- Confusing cotangent with other trigonometric functions like tangent or cosecant.
- Forgetting to include the constant ( C ) of integration.
- Not properly applying the substitution method, particularly not changing the limits of integration if it's a definite integral.
AI-generated content may contain errors. Please verify critical information