∫ cos(ln x) dx
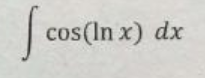
Understand the Problem
The question is asking to find the integral of the function cos(ln x) with respect to x. This will involve integration techniques and possibly substitution methods.
Answer
The final result is: $$ \int \cos(\ln x) \, dx = x \left(\sin(\ln x) + \frac{1}{2}\cos(\ln x)\right) + C $$
Answer for screen readers
The final answer is: $$ \int \cos(\ln x) , dx = e^{\ln x} \left(\sin(\ln x) + \frac{1}{2}\cos(\ln x)\right) + C = x \left(\sin(\ln x) + \frac{1}{2}\cos(\ln x)\right) + C $$
Steps to Solve
-
Substitution Let ( u = \ln x ). Then, the derivative ( du = \frac{1}{x} dx ) or ( dx = x , du = e^u , du ) since ( x = e^u ).
-
Change of Variables in the Integral Substituting ( u ) into the integral gives: $$ \int \cos(\ln x) , dx = \int \cos(u) \cdot e^u , du $$
-
Integrating by Parts Use integration by parts where ( v = e^u ) and ( dv = \cos(u) , du ). Let ( dv = \cos(u) , du ) and ( v = \sin(u) ).
-
Applying Integration by Parts Formula The integration by parts formula is given by: $$ \int v , du = uv - \int u , dv $$ So, we apply it: $$ \int e^u \cos(u) , du = e^u \sin(u) - \int e^u \sin(u) , du $$
-
Integrating the Remaining Integral Now we have the remaining integral ( \int e^u \sin(u) , du ), which again will use integration by parts: Set ( v = e^u ) and ( dv = \sin(u) , du ). After performing integration by parts, we will use a technique to combine the results.
-
Combining Results to Solve for the Integral We will have: $$ I = \int e^u \cos(u) , du $$ and a second integral ( J = \int e^u \sin(u) , du ). The relationship leads us to a system of equations, which we can solve to find ( I ).
-
Final Substitution Once we calculate ( I ) and ( J ), we substitute back ( u = \ln x ) to find the final answer in terms of ( x ).
The final answer is: $$ \int \cos(\ln x) , dx = e^{\ln x} \left(\sin(\ln x) + \frac{1}{2}\cos(\ln x)\right) + C = x \left(\sin(\ln x) + \frac{1}{2}\cos(\ln x)\right) + C $$
More Information
This integral utilizes both substitution and integration by parts techniques. The result highlights the interplay between exponential and trigonometric functions, which occurs frequently in calculus problems.
Tips
- Forgetting to change the limits of integration when substituting variables.
- Not applying integration by parts correctly or mismanaging the components of ( u ) and ( dv ).
- Failing to substitute back to the original variable at the end.
AI-generated content may contain errors. Please verify critical information