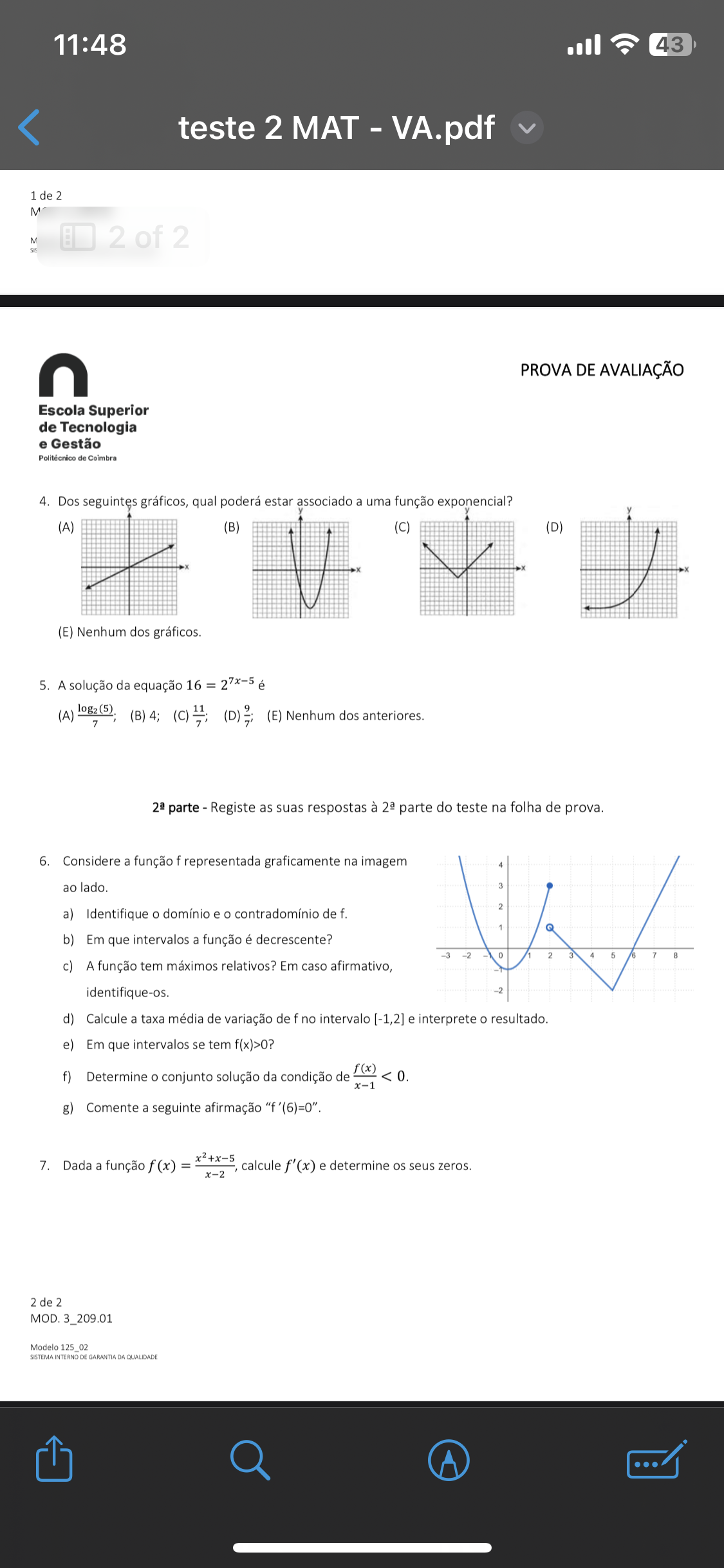
Considere a função f representada graficamente na imagem ao lado. a) Identifique o domínio e o contradomínio de f. b) Em que intervalos a função é decrescente? c) A função tem máxi... Considere a função f representada graficamente na imagem ao lado. a) Identifique o domínio e o contradomínio de f. b) Em que intervalos a função é decrescente? c) A função tem máximos relativos? Em caso afirmativo, identifique-os. d) Calcule a taxa média de variação de f no intervalo [-1,2] e interprete o resultado. e) Em que intervalos se tem f(x)>0? f) Determine o conjunto solução da condição de f(x)/(x-1) < 0. g) Comente a seguinte afirmação 'f'(6)=0'. Dada a função f(x) = (x^2 + x - 5)/(x - 2), calcule f'(x) e determine os seus zeros.
Understand the Problem
A questão envolve a interpretação de gráficos e análise de funções matemáticas, incluindo identificação de domínios, intervalos de crescimento e decrescimento, cálculo de taxas de variação, e derivadas.
Answer
Domínio: $[-3, 7]$, Contradomínio: $[-2, 0]$; Decréscimos: $[-3, 0]$ e $[3, 7]$; Máximo: $(0,0)$; Taxa média: $\frac{1}{3}$; $f(x) > 0$ em $(0, 3)$; $f(x) < 0$ em $[-2, 0]$; $f'(6)=0$ indica ponto crítico.
Answer for screen readers
- Domínio: $[-3, 7]$; Contradomínio: $[-2, 0]$
- Decréscimos: $[-3, 0]$ e $[3, 7]$
- Máximo relativo em $(0, 0)$
- Taxa média de variação: $\frac{1}{3}$
- Intervalos: $(0, 3)$ onde $f(x) > 0$
- $f(x) < 0$ em $[-2, 0]$
- $f'(6)=0$ indica um ponto crítico.
Steps to Solve
-
Identificação do domínio e contradomínio Identificamos o domínio da função $f(x)$ como todos os valores de $x$ que a função pode assumir. Pela análise do gráfico, o domínio é $[-3, 7]$. O contradomínio é o conjunto de valores que $f(x)$ pode atingir, que é $[-2, 0]$.
-
Intervalos de decréscimo Analisaremos o gráfico para ver onde a função está caindo. Observamos que a função é decrecente no intervalo $[-3, 0]$ e $[3, 7]$.
-
Máximos relativos Verificamos se existem máximos relativos. O gráfico mostra um máximo relativo no ponto $x = 0$. Assim, podemos afirmar que a função possui um máximo relativo em $(0, 0)$.
-
Cálculo da taxa média de variação A taxa média de variação de $f(x)$ no intervalo $[-1, 2]$ é dada pela fórmula: $$ \text{Taxa média} = \frac{f(2) - f(-1)}{2 - (-1)} $$ Calculamos $f(2)$ e $f(-1)$ a partir do gráfico. Assim, obtemos: $$ f(2) = -1, ; f(-1) = -2 $$ Logo, a taxa média é: $$ \text{Taxa média} = \frac{-1 - (-2)}{2 + 1} = \frac{1}{3} $$
-
Intervalos onde $f(x) > 0$ Observamos graficamente e verificamos que $f(x) > 0$ no intervalo $(0, 3)$.
-
Solução da condição de $f(x) < 0$ Determinamos quando $f(x) < 0$ no gráfico. O resultado é que $f(x) < 0$ no intervalo $[-2, 0]$.
-
Comentário sobre $f'(6)=0$ O que significa $f'(6)=0$ é que a inclinação da tangente à curva em $x=6$ é zero, indicando um ponto crítico na função.
- Domínio: $[-3, 7]$; Contradomínio: $[-2, 0]$
- Decréscimos: $[-3, 0]$ e $[3, 7]$
- Máximo relativo em $(0, 0)$
- Taxa média de variação: $\frac{1}{3}$
- Intervalos: $(0, 3)$ onde $f(x) > 0$
- $f(x) < 0$ em $[-2, 0]$
- $f'(6)=0$ indica um ponto crítico.
More Information
Os conceitos abordados são fundamentais na análise de funções, permitindo entender o comportamento das mesmas em diferentes intervalos. Máximos, mínimos, e intervalos de crescimento e decrescimento são cruciais para a interpretação gráfica.
Tips
- Não identificar corretamente o domínio e contradomínio a partir do gráfico.
- Falhar em calcular a taxa média de variação ao esquecer de aplicar a fórmula corretamente.
- Não verificar todos os intervalos onde a função é positiva ou negativa.
AI-generated content may contain errors. Please verify critical information