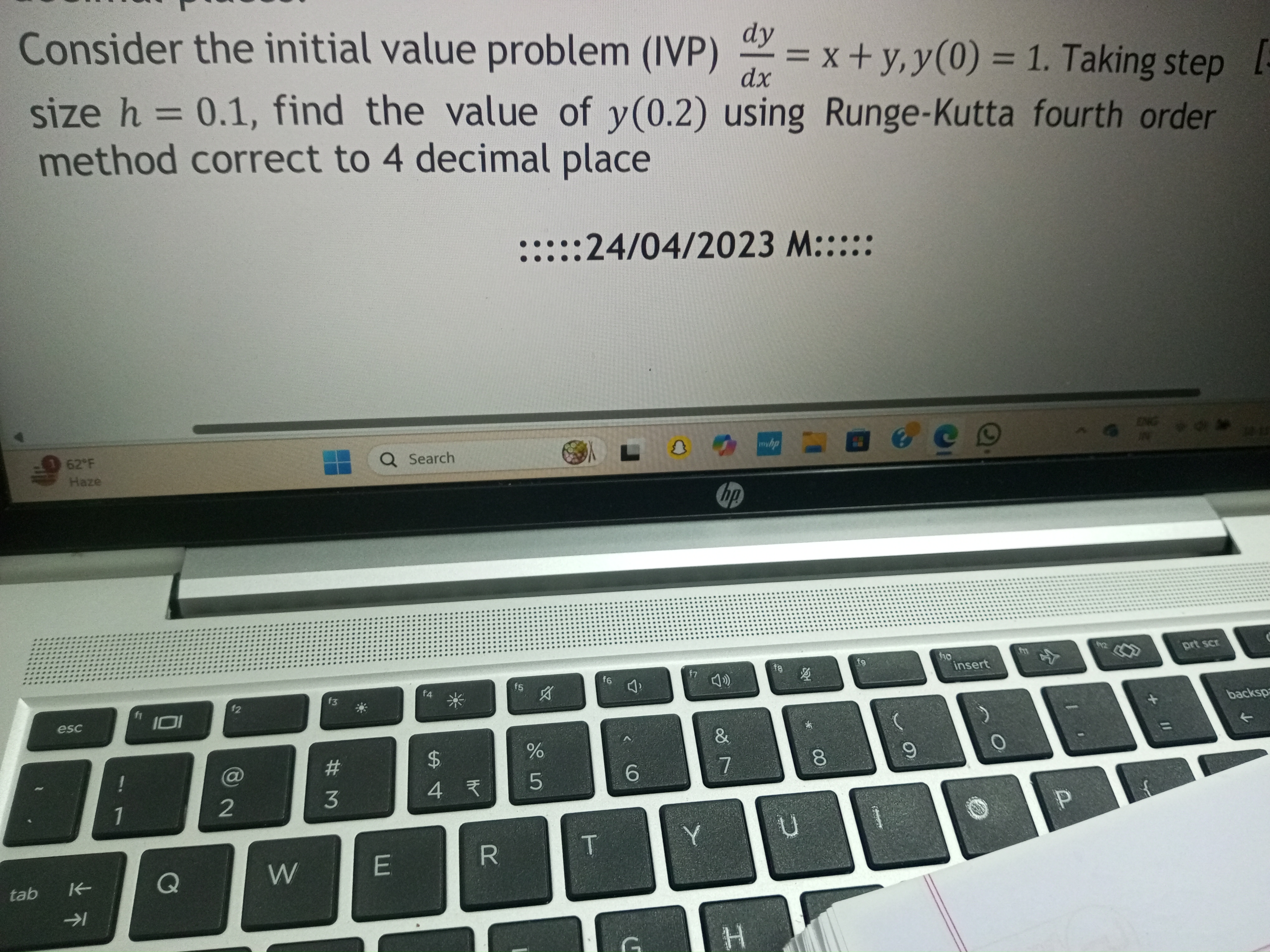
Consider the initial value problem (IVP) dy/dx = x + y, y(0) = 1. Taking step size h = 0.1, find the value of y(0.2) using Runge-Kutta fourth order method correct to 4 decimal plac... Consider the initial value problem (IVP) dy/dx = x + y, y(0) = 1. Taking step size h = 0.1, find the value of y(0.2) using Runge-Kutta fourth order method correct to 4 decimal places.
Understand the Problem
The question is asking to solve an initial value problem using the Runge-Kutta fourth order method. It requires finding the value of y at x=0.2 given the differential equation and the initial condition. The result should be accurate to four decimal places.
Answer
The value of \( y(0.2) \) is approximately \( 1.2426 \).
Answer for screen readers
The value of ( y(0.2) ) is approximately ( 1.2426 ).
Steps to Solve
- Define the function and the initial condition
The given differential equation is ( \frac{dy}{dx} = x + y ) with the initial condition ( y(0) = 1 ). We can identify this as ( f(x, y) = x + y ).
- Set the parameters
We have a step size ( h = 0.1 ), and we need to compute ( y ) at ( x = 0.2 ). Therefore, we will perform 2 iterations since ( 0.2 / 0.1 = 2 ).
- First Iteration (from ( x = 0 ) to ( x = 0.1 ))
Calculate the intermediate values ( k_1, k_2, k_3, k_4 ):
[ k_1 = h f(x_n, y_n) = 0.1 \cdot f(0, 1) = 0.1 \cdot (0 + 1) = 0.1 ]
[ k_2 = h f\left(x_n + \frac{h}{2}, y_n + \frac{k_1}{2}\right) = 0.1 \cdot f\left(0.05, 1.05\right) = 0.1 \cdot (0.05 + 1.05) = 0.11 ]
[ k_3 = h f\left(x_n + \frac{h}{2}, y_n + \frac{k_2}{2}\right) = 0.1 \cdot f\left(0.05, 1.055\right) = 0.1 \cdot (0.05 + 1.055) = 0.1105 ]
[ k_4 = h f(x_n + h, y_n + k_3) = 0.1 \cdot f(0.1, 1.1105) = 0.1 \cdot (0.1 + 1.1105) = 0.12105 ]
Now, use the ( k ) values to update ( y ):
[ y_{n+1} = y_n + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4) ]
Substituting the values:
[ y_{1} = 1 + \frac{1}{6}(0.1 + 2 \cdot 0.11 + 2 \cdot 0.1105 + 0.12105) = 1 + \frac{1}{6}(0.1 + 0.22 + 0.221 + 0.12105) = 1 + \frac{0.66205}{6} \approx 1.1103 ]
- Second Iteration (from ( x = 0.1 ) to ( x = 0.2 ))
Now repeat the process for ( n = 1 ):
[ k_1 = h f(0.1, 1.1103) = 0.1 \cdot (0.1 + 1.1103) = 0.12103 ]
[ k_2 = h f\left(0.15, 1.1103 + \frac{0.12103}{2}\right) = 0.1 \cdot f(0.15, 1.171315) = 0.1 \cdot (0.15 + 1.171315) = 0.1321315 ]
[ k_3 = h f\left(0.15, 1.1103 + \frac{0.1321315}{2}\right) = 0.1 \cdot f(0.15, 1.17186575) = 0.1 \cdot (0.15 + 1.17186575) = 0.132186575 ]
[ k_4 = h f(0.2, 1.1103 + 0.132186575) = 0.1 \cdot f(0.2, 1.242486575) = 0.1 \cdot (0.2 + 1.242486575) = 0.1442486575 ]
Update ( y ):
[ y_{2} = y_{1} + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4) ]
Substituting values:
[ y_{2} = 1.1103 + \frac{1}{6}(0.12103 + 2 \cdot 0.1321315 + 2 \cdot 0.132186575 + 0.1442486575) ]
Calculating:
[ y_{2} \approx 1.1103 + \frac{1}{6}(0.12103 + 0.264263 + 0.26437315 + 0.1442486575) = 1.1103 + \frac{0.7939148075}{6} \approx 1.1103 + 0.132318 ]
Thus, ( y(0.2) \approx 1.2426 ).
The value of ( y(0.2) ) is approximately ( 1.2426 ).
More Information
Using the Runge-Kutta fourth order method provides a highly accurate estimate of the solution of the initial value problem. This method gives better results compared to simpler methods like Euler's method, especially for non-linear equations.
Tips
- Forgetting to calculate midpoints correctly: Ensure that the ( k ) values are calculated based on the proper ( x ) and ( y ) values.
- Not using the correct average in the final step: Remember to use the weighted average of ( k_1, k_2, k_3, k_4 ) properly when updating ( y ).
AI-generated content may contain errors. Please verify critical information