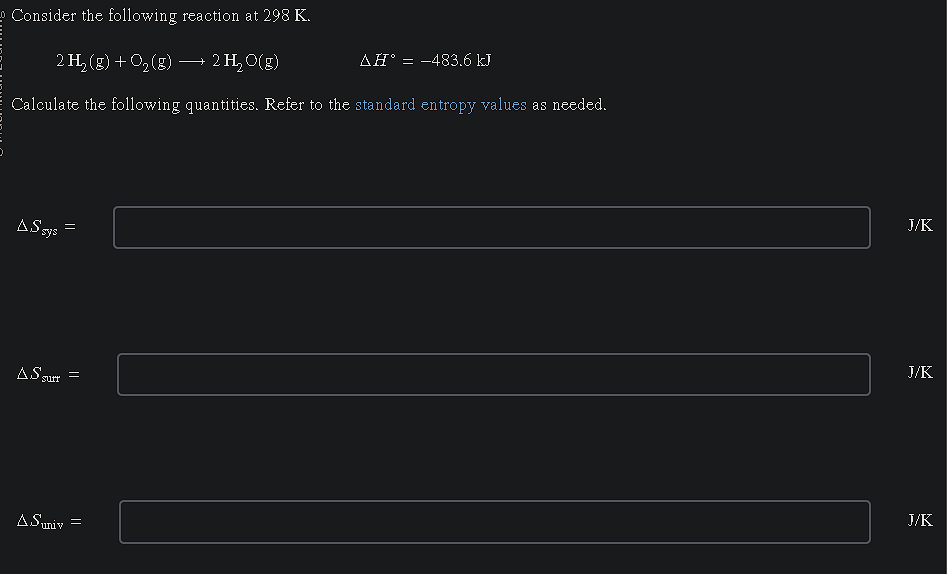
Consider the following reaction at 298 K. 2 H2(g) + O2(g) → 2 H2O(g) ΔH° = -483.6 kJ Calculate the following quantities. ΔS_sys = , ΔS_surr = , ΔS_univ =

Steps to Solve

1. Calculate ΔS_sys (System Entropy Change)

To find the entropy change of the system ($\Delta S_{sys}$), use the standard entropy values for the reactants and products. The formula is:

$$ \Delta S_{sys} = \sum S^\circ_{products} - \sum S^\circ_{reactants} $$

From standard entropy tables, assume the following values (in J/K·mol):

• $S^\circ(H_2(g)) = 130.6$
• $S^\circ(O_2(g)) = 205.0$
• $S^\circ(H_2O(g)) = 188.8$

For the reaction:

$$ \Delta S_{sys} = [2 \cdot S^\circ(H_2O)] - [2 \cdot S^\circ(H_2) + S^\circ(O_2)] $$

2. Plug in the values

Now substituting in the values:

$$ \Delta S_{sys} = [2 \cdot 188.8] - [2 \cdot 130.6 + 205.0] $$

Calculating it:

$$ \Delta S_{sys} = 377.6 - (261.2 + 205.0) $$ $$ \Delta S_{sys} = 377.6 - 466.2 $$ $$ \Delta S_{sys} = -88.6 , \text{J/K} $$

3. Calculate ΔS_surr (Surroundings Entropy Change)

The entropy change of the surroundings ($\Delta S_{surr}$) can be calculated using the enthalpy change ($\Delta H^\circ$) and the temperature (T):

$$ \Delta S_{surr} = -\frac{\Delta H^\circ}{T} $$

Substituting the values:

$$ \Delta S_{surr} = -\frac{-483600 , \text{J}}{298 , \text{K}} $$

4. Simplify the equation

Calculating:

$$ \Delta S_{surr} = \frac{483600}{298} = 1622.15 , \text{J/K} $$

5. Calculate ΔS_univ (Total Entropy Change)

The total entropy change of the universe ($\Delta S_{univ}$) is the sum of $\Delta S_{sys}$ and $\Delta S_{surr}$:

$$ \Delta S_{univ} = \Delta S_{sys} + \Delta S_{surr} $$

Substituting in:

$$ \Delta S_{univ} = -88.6 + 1622.15 $$

6. Final Calculation

Calculating the total:

$$ \Delta S_{univ} = 1533.55 , \text{J/K} $$