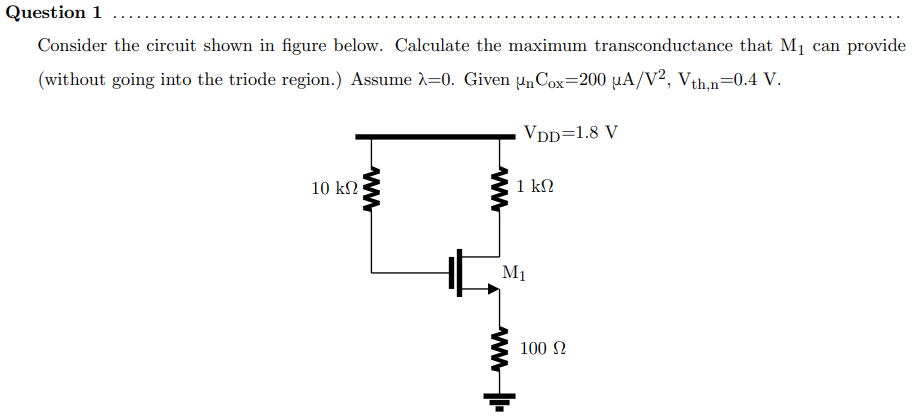
Consider the circuit shown in the figure. Calculate the maximum transconductance that M1 can provide (without going into the triode region.) Assume λ=0. Given µnCox=200 μA/V^2, Vth... Consider the circuit shown in the figure. Calculate the maximum transconductance that M1 can provide (without going into the triode region.) Assume λ=0. Given µnCox=200 μA/V^2, Vth,n=0.4 V.
Understand the Problem
The question asks to calculate the maximum transconductance of a MOSFET (M1) in a given circuit, operating in saturation region (not triode), with given parameters such as μnCox, threshold voltage (Vth,n), and assuming channel-length modulation (λ) is zero. This will involve understanding MOSFET characteristics in saturation and how transconductance relates to drain current and gate-source voltage.
Answer
$g_{m,max} = 400 \mu S$
Answer for screen readers
$g_{m,max} = 400 \mu S$
Steps to Solve
-
Determine the maximum drain current ($I_{D,max}$)
The maximum drain current $I_{D,max}$ occurs when the MOSFET is at the edge of the triode region. This happens when $V_{DS} = V_{GS} - V_{th,n}$. The drain current can be calculated by considering the voltage drop across the $1k\Omega$ resistor and the $100\Omega$ resistor. When the MOSFET is at the edge of triode region, the drain voltage can be expressed as $V_D = V_{DD} - I_{D,max} * 1k\Omega$. Also, the source voltage is given by $V_S = I_{D,max} * 100\Omega$.
-
Express $V_{DS}$ and $V_{GS}$ in terms of $I_{D,max}$
$V_{DS} = V_D - V_S = V_{DD} - I_{D,max} * 1k\Omega - I_{D,max} * 100\Omega = 1.8 - 1000I_{D,max} - 100I_{D,max} = 1.8 - 1100I_{D,max}$
$V_G = V_{DD} = 1.8V$. Therefore, $V_{GS} = V_G - V_S = 1.8 - I_{D,max} * 100\Omega$.
-
Set $V_{DS} = V_{GS} - V_{th,n}$ and solve for $I_{D,max}$
We know that $V_{DS} = V_{GS} - V_{th,n}$ at the edge of triode region. Consequently, we have: $1.8 - 1100I_{D,max} = 1.8 - 100I_{D,max} - 0.4$. This simplifies to: $1000I_{D,max} = 0.4$ Therefore, $I_{D,max} = \frac{0.4}{1000} = 0.0004 A = 400\mu A$.
-
Calculate $g_{m,max}$
The transconductance $g_m$ in saturation region is given by $g_m = \sqrt{2\mu_n C_{ox} \frac{W}{L} I_D}$. Also, $I_D = \frac{1}{2}\mu_n C_{ox} \frac{W}{L}(V_{GS} - V_{th,n})^2$ and $g_m = \mu_n C_{ox} \frac{W}{L}(V_{GS} - V_{th,n})$. From these two equations, we can write: $g_m = \sqrt{2\mu_n C_{ox} (\frac{W}{L}) I_D}=2*\frac{I_D}{V_{GS}-V_{th}}$. Also, $g_m =\sqrt{2 \mu_n C_{ox} I_D}$. Therefore, using $\mu_n C_{ox}=200 \mu A/V^2$ and $I_{D,max} = 400 \mu A$:
$g_{m,max} = \sqrt{2 * 200 \mu A/V^2 * 400 \mu A} = \sqrt{160000 (\mu A)^2/V^2} = \sqrt{16 * 10^4 * 10^{-12} A^2/V^2} = \sqrt{16} * 10^{-4} A/V = 4 * 10^{-4} A/V = 400 \mu S$
$g_{m,max} = 400 \mu S$
More Information
The maximum transconductance is $400 \mu S$, which occurs at the boundary between the saturation and triode regions. This represents the highest gain the transistor can provide in this circuit configuration.
Tips
A common mistake is not correctly determining the drain current at the edge of the triode region by setting $V_{DS} = V_{GS} - V_{th,n}$. Another mistake is using the wrong formula for $g_m$. Also, unit conversions can be a source of error if not handled carefully.
AI-generated content may contain errors. Please verify critical information