Consider an ideal gas with rho * mg / c * m^3 at = 38/18 standard pressure and temperature. If the speed of sound propagation in this gas is v = 330 m/s, the degree of freedom of t... Consider an ideal gas with rho * mg / c * m^3 at = 38/18 standard pressure and temperature. If the speed of sound propagation in this gas is v = 330 m/s, the degree of freedom of the gas is 5. Then the value of 10p is (nearest integer).
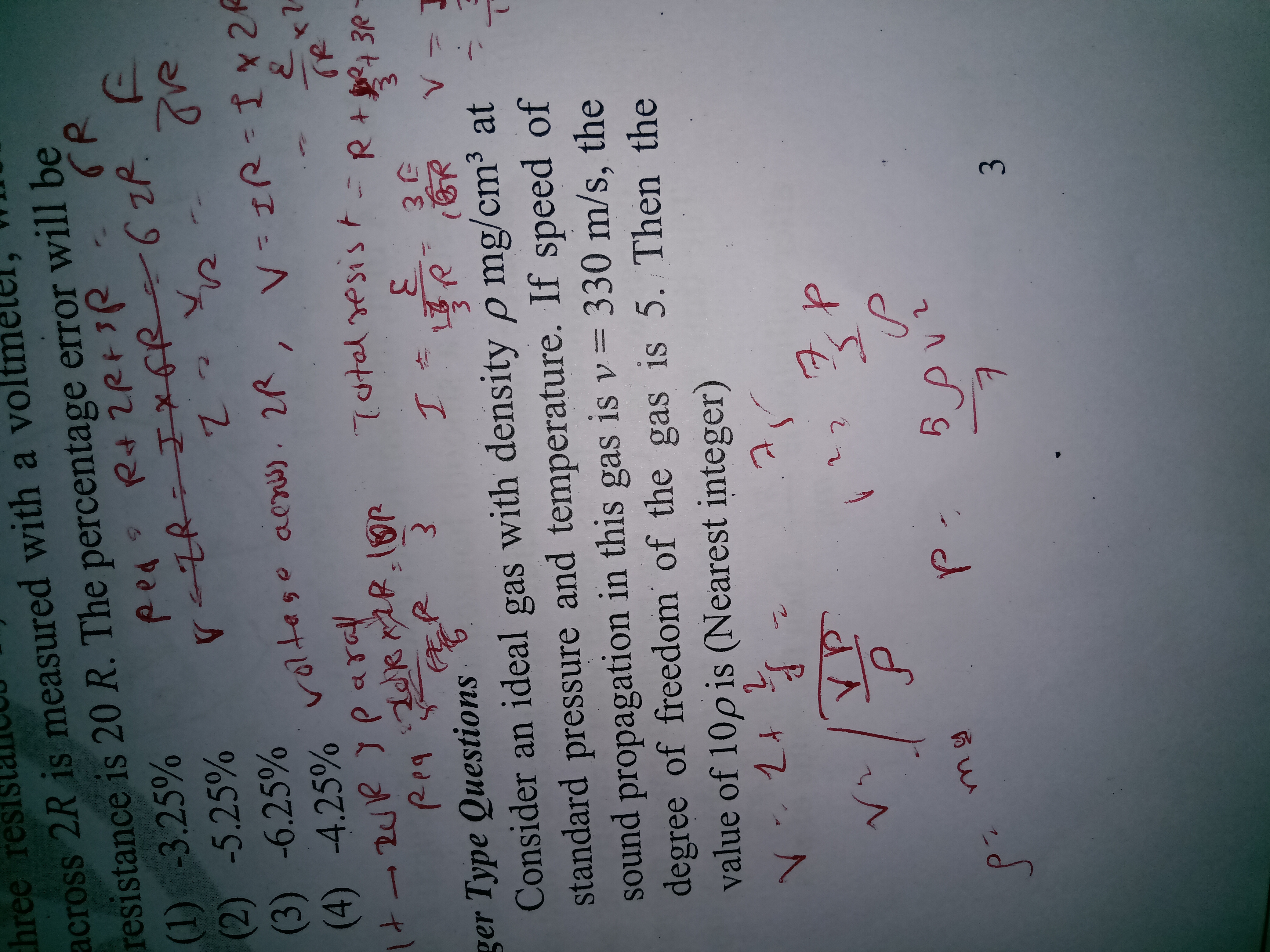
Understand the Problem
The question involves calculating the pressure of an ideal gas based on the given parameters such as speed of sound, density, and degrees of freedom. It uses the relationship between these variables to find the value of 10p.
Answer
The calculation for \( 10p \) relies on the density used; derive \( p \) as \( p = \frac{(350)^2 \cdot \rho}{1.4} \) and compute \( 10p \).
Answer for screen readers
The final answer for ( 10p ) will depend on the value of ( \rho ) used in the calculations.
Steps to Solve
-
Identify Given Parameters
The problem involves the speed of sound ( v ), density ( \rho ), and the degrees of freedom ( f ). In this case, we have ( v = 350 , \text{m/s} ). -
Relationship Between Speed of Sound and Pressure
The speed of sound in an ideal gas is calculated using the formula:
$$ v = \sqrt{\frac{\gamma p}{\rho}} $$
where ( \gamma ) represents the ratio of specific heats (for a diatomic gas, ( \gamma \approx 1.4 )), ( p ) is the pressure, and ( \rho ) is the density. -
Rearranging the Formula to Find Pressure
Rearranging the equation gives us:
$$ p = \frac{v^2 \rho}{\gamma} $$ -
Substituting the Known Values
We need to find the density ( \rho ) of the gas. Assume it has a certain value when conditions are given (you may need the value from your notes). Then substitute ( v ) and ( \rho ) into:
$$ p = \frac{(350 , \text{m/s})^2 \cdot \rho}{1.4} $$ -
Calculation of Pressure
After substituting in the density value, compute the above equation to find the pressure ( p ). -
Finding ( 10p )
Finally, calculate ( 10p ) by multiplying the found pressure ( p ) by 10.
The final answer for ( 10p ) will depend on the value of ( \rho ) used in the calculations.
More Information
To solve for pressure in an ideal gas, you utilize the speed of sound and density. The derived relationship shows how these variables interact in a thermal context.
Tips
- Forgetting to convert units appropriately.
- Misapplying the value of ( \gamma ) for different gases; ensure you use ( \gamma = 1.4 ) for diatomic gases correctly.
- Not rearranging the equation properly.
AI-generated content may contain errors. Please verify critical information