Complete the square to re-write the quadratic function in vertex form: y = x² + 10x - 6
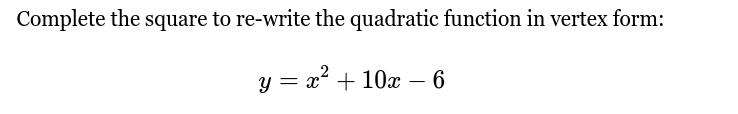
Understand the Problem
The question is asking to complete the square for the given quadratic function and rewrite it in vertex form.
Answer
The vertex form is $$ y = (x + 5)^2 - 31 $$
Answer for screen readers
The vertex form of the quadratic function is
$$ y = (x + 5)^2 - 31 $$
Steps to Solve
- Identify coefficients
The given quadratic function is ( y = x^2 + 10x - 6 ).
Here, the coefficient of ( x^2 ) is 1, and we need to focus on the linear term ( 10x ).
- Complete the square for the quadratic part
To complete the square, take half of the coefficient of the ( x ) term (( 10 )), square it, and add/subtract it inside the equation.
Half of ( 10 ) is ( 5 ), and squaring it gives ( 5^2 = 25 ).
- Rewrite the quadratic part
Now we can rewrite ( x^2 + 10x ) as:
$$ x^2 + 10x = (x + 5)^2 - 25 $$
This maintains equality, as we're subtracting the ( 25 ) we added.
- Substitute back into the equation
Substituting back into the original equation, we have:
$$ y = (x + 5)^2 - 25 - 6 $$
- Simplify the equation
Now combine the constants:
$$ -25 - 6 = -31 $$
Thus, the equation becomes:
$$ y = (x + 5)^2 - 31 $$
- Final Vertex Form
The vertex form of the quadratic function is:
$$ y = (x + 5)^2 - 31 $$
This shows the vertex of the parabola is at the point ( (-5, -31) ).
The vertex form of the quadratic function is
$$ y = (x + 5)^2 - 31 $$
More Information
The vertex form of a quadratic function is ( y = a(x - h)^2 + k ), where ( (h, k) ) is the vertex of the parabola. In this case, the vertex is at ( (-5, -31) ). Completing the square helps us find the vertex easily and understand the graph's transformation.
Tips
- Not correctly finding half of the linear coefficient: Make sure to always divide by 2 when obtaining half.
- Forgetting to adjust the constant term: Remember to add and subtract the square value inside the function to keep the equation balanced.
AI-generated content may contain errors. Please verify critical information