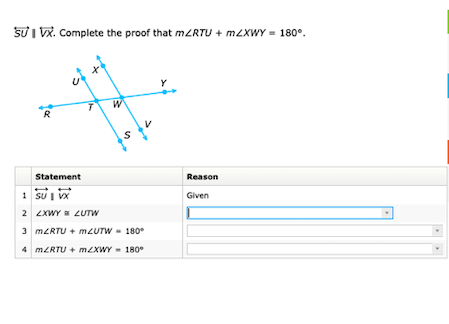
Complete the proof that m∠RTU + m∠XWY = 180°.
Understand the Problem
The question is asking to complete a proof that establishes the relationship between angles formed by two parallel lines cut by a transversal. It requires understanding properties of parallel lines and angles, specifically the corresponding angles or alternate interior angles that sum up to 180 degrees.
Answer
The relationship established is $m\angle RTU + m\angle XYW = 180^\circ$.
Answer for screen readers
The proof shows that $m\angle RTU + m\angle XYW = 180^\circ$.
Steps to Solve
-
Identify Given Information The problem states that $\overline{SU} \parallel \overline{VX}$. This establishes that the two lines are parallel, leading to specific angle properties.
-
Examine Relevant Angles Since $\overline{SU}$ is parallel to $\overline{VX}$, and they are cut by transversal $\overline{XY}$, we know certain angles are equal. Here, $\angle XYW \cong \angle LUT$ because they are alternate interior angles.
-
Add Angles Together From the equality of alternate interior angles, we have: $$ m\angle XYW = m\angle LUT $$
-
Write the Angle Sum Property Using the properties of angles formed by a straight line, we know that $\angle RTU$ and $\angle XYW$ are supplementary angles, which means they add up to $180^\circ$: $$ m\angle RTU + m\angle XYW = 180^\circ $$
-
Substitute Known Angles Substituting the previous result into the equation gives us the final relationship: $$ m\angle RTU + m\angle LUT = 180^\circ $$
The proof shows that $m\angle RTU + m\angle XYW = 180^\circ$.
More Information
This proof relies heavily on the properties of angles formed when a transversal crosses parallel lines, specifically utilizing the properties of alternate interior angles and how adjacent angles formed in a linear pair sum to $180^\circ$.
Tips
- Misidentifying angles: Always check if the angles you refer to are indeed alternate interior or corresponding angles.
- Forgetting that alternate interior angles are equal: This is a critical property whenever dealing with parallel lines and transversals.
AI-generated content may contain errors. Please verify critical information