Combine like terms: x^2 + 4 + 5y^3 + 2x^2 - 2x^2 - 6 + 1

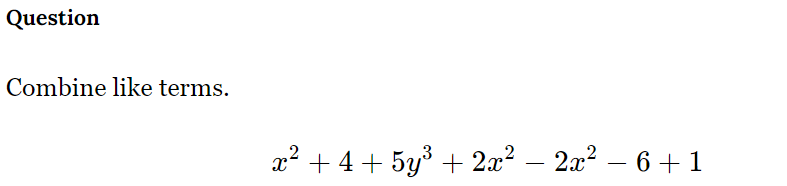
Understand the Problem

The question is asking to combine like terms in the given polynomial expression. We will identify and sum up the coefficients of the like terms to simplify the expression.

Answer

The simplified expression is $x^2 + 5y^3 - 1$.

Steps to Solve

Identify like terms

First, identify the like terms in the expression:

The $x^2$ terms: $x^2$, $2x^2$, and $-2x^2$.
The constant terms: $4$, $-6$, and $1$.
The $y^3$ term: $5y^3$.

Combine the $x^2$ terms

Now, combine the $x^2$ terms:

$$ x^2 + 2x^2 - 2x^2 = (1 + 2 - 2)x^2 = 1x^2 = x^2 $$

Combine the constant terms

Next, combine the constant terms:

$$ 4 - 6 + 1 = (4 - 6 + 1) = -1 $$

Write the simplified expression

Finally, combine the results:

$$ x^2 + 5y^3 - 1 $$

The simplified expression is $x^2 + 5y^3 - 1$.

More Information

Combining like terms allows for simplification of polynomial expressions, making them easier to work with in algebra. Recognizing and summing coefficients of like terms is a fundamental skill in algebra.

Tips

Forgetting to include all like terms when combining. Always double-check to ensure all similar terms are accounted for.
Incorrectly adding or subtracting coefficients. Pay close attention to signs.

Thank you for voting!