Combine like terms: 2 - 4y - 7y² + 5y² + 5 + 4y - 2y.
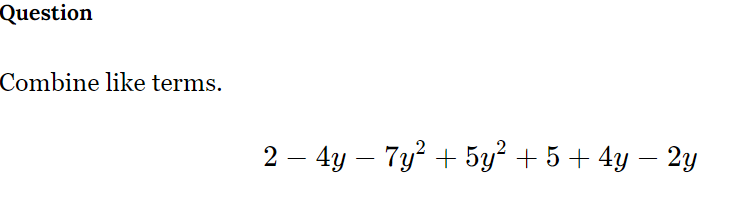
Understand the Problem
The question is asking us to simplify the given expression by combining like terms. This involves identifying terms with the same variable and degree and then adding or subtracting their coefficients.
Answer
The simplified expression is \(7 - 2y - 2y^2\).
Answer for screen readers
The simplified expression is (7 - 2y - 2y^2).
Steps to Solve
- Identify Like Terms
Group the like terms in the expression:
- Constant terms: (2) and (5)
- Linear terms (terms with (y)): (-4y), (4y), and (-2y)
- Quadratic terms (terms with (y^2)): (-7y^2) and (5y^2)
- Combine the Constant Terms
Add the constant terms: $$ 2 + 5 = 7 $$
- Combine the Linear Terms
Combine the terms with (y): $$ -4y + 4y - 2y = 0y - 2y = -2y $$
- Combine the Quadratic Terms
Add the quadratic terms: $$ -7y^2 + 5y^2 = -2y^2 $$
- Write the Final Expression
Combine all the results: $$ 7 - 2y - 2y^2 $$
The simplified expression is (7 - 2y - 2y^2).
More Information
Combining like terms is a fundamental skill in algebra that allows for the simplification of expressions, making calculations easier and clearer.
Tips
- Forgetting to combine all terms: Ensure all like terms are accounted for.
- Mixing up positive and negative signs when combining: Double-check your addition and subtraction of coefficients.
Thank you for voting!
