چگالی توزیع زیر را در نظر بگیرید. f(x, y) = { 2c y (1 - x); 0 ≤ y ≤ x ≤ 1 0; ow ; c مطلوب است.
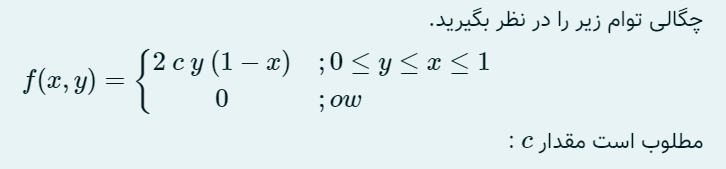
Understand the Problem
سوال در مورد تعیین مقدار یک ثابت در یک تابع احتمال مشترک است. باید از شرایط داده شده در تابع و ویژگیهای توزیع احتمال استفاده کنیم.
Answer
\( c = 12 \)
Answer for screen readers
مقدار ثابت ( c ) برابر است با ( 12 ).
Steps to Solve
- شرط نرمالیزاسیون توزیع احتمال برای یافتن مقدار ثابت ( c )، ابتدا باید دوگانه توزیع احتمال را بر روی دامنه مورد نظر ادغام کنیم تا مطمئن شویم که نرمالیزه است، یعنی مجموع سطح زیر منحنی برابر با 1 باشد. بنابراین باید محاسبه کنیم:
$$ \int_0^1 \int_0^x f(x,y) , dy , dx = 1 $$
- جایگذاری تابع در انتگرال تابع مشترک احتمال را در انتگرال جایگذاری میکنیم:
$$ \int_0^1 \int_0^x 2 c y (1 - x) , dy , dx $$
- محاسبه انتگرال داخلی ابتدا انتگرال داخلی را نسبت به ( y ) محاسبه میکنیم:
$$ \int_0^x 2 c y (1 - x) , dy = 2 c (1 - x) \left[ \frac{y^2}{2} \right]_0^x = 2 c (1 - x) \left( \frac{x^2}{2} \right) = c x^2 (1 - x) $$
- محاسبه انتگرال خارجی حالا باید انتگرال خارجی را محاسبه کنیم:
$$ \int_0^1 c x^2 (1 - x) , dx $$
این انتگرال را میتوان به دو بخش تقسیم کرد:
$$ c \int_0^1 (x^2 - x^3) , dx $$
حالا هر بخش انتگرال را محاسبه میکنیم:
$$ \int x^2 , dx = \frac{x^3}{3} \Big|_0^1 = \frac{1}{3} $$ $$ \int x^3 , dx = \frac{x^4}{4} \Big|_0^1 = \frac{1}{4} $$
- جایگذاری نتایج انتگرالها نتایج را جایگذاری میکنیم:
$$ c \left( \frac{1}{3} - \frac{1}{4} \right) = c \left( \frac{4}{12} - \frac{3}{12} \right) = c \frac{1}{12} $$
- برابر کردن با 1 برای نرمالیزه شدن، نتیجه باید برابر با 1 باشد:
$$ c \frac{1}{12} = 1 $$
- حل برای ( c ) بنابراین:
$$ c = 12 $$
مقدار ثابت ( c ) برابر است با ( 12 ).
More Information
ثابت ( c ) در توزیعهای دوبعدی به گونهای انتخاب میشود که مجموع تمام احتمالها برابر با 1 باشد. در این مثال، ما از نرمالیزاسیون توزیعهای احتمال استفاده کردیم.
Tips
- نادیده گرفتن محدودیتهای دامنه ( 0 \leq y \leq x \leq 1 ) هنگام محاسبه انتگرال.
- عدم توجه به نرمالیزاسیون در انتهای محاسبات.
AI-generated content may contain errors. Please verify critical information