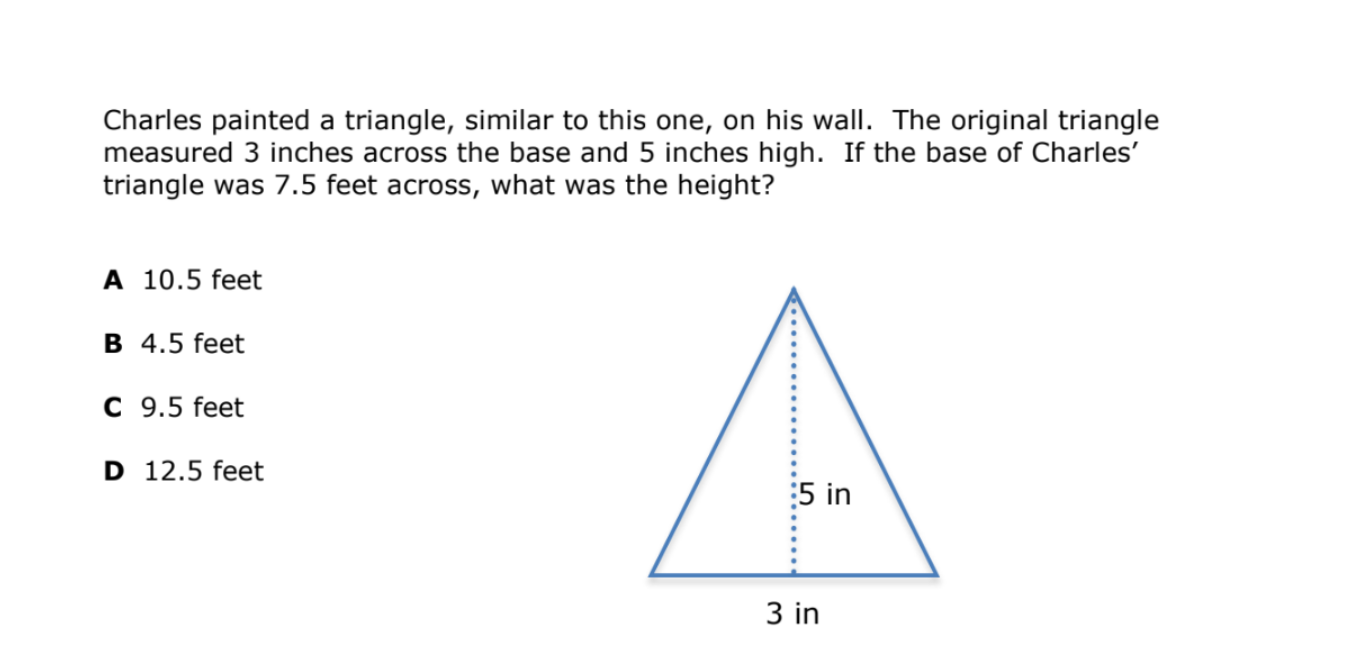
Charles painted a triangle, similar to one with a base of 3 inches and a height of 5 inches. If the base of Charles' triangle is 7.5 feet, what is the height?

Steps to Solve

1. Convert the base of the larger triangle to inches. Since the smaller triangle's dimensions are in inches, convert the base of Charles' triangle from feet to inches. There are 12 inches in a foot, so: $7.5 \text{ feet} \times 12 \frac{\text{inches}}{\text{foot}} = 90 \text{ inches}$

2. Set up a proportion to find the height of the larger triangle. Because the triangles are similar, the ratio of their corresponding sides is equal. We can set up the following proportion, where $h$ is the height of the larger triangle in inches: $\frac{\text{height of smaller triangle}}{\text{base of smaller triangle}} = \frac{\text{height of larger triangle}}{\text{base of larger triangle}}$ $\frac{5 \text{ inches}}{3 \text{ inches}} = \frac{h \text{ inches}}{90 \text{ inches}}$

3. Solve for $h$. Cross-multiply to solve for $h$: $5 \times 90 = 3 \times h$ $450 = 3h$ $h = \frac{450}{3} = 150 \text{ inches}$

4. Convert the height of the larger triangle back to feet. Divide the height in inches by 12 to convert it to feet: $150 \text{ inches} \div 12 \frac{\text{inches}}{\text{foot}} = 12.5 \text{ feet}$